किसी चुंबकीय द्विध्रुव के कारण किसी स्वेच्छ बिंदु $P (r, θ)$ पर चुंबकीय क्षेत्र का व्यंजक प्राप्त करे ।

Video Solution

Text Solution

Verified by Experts

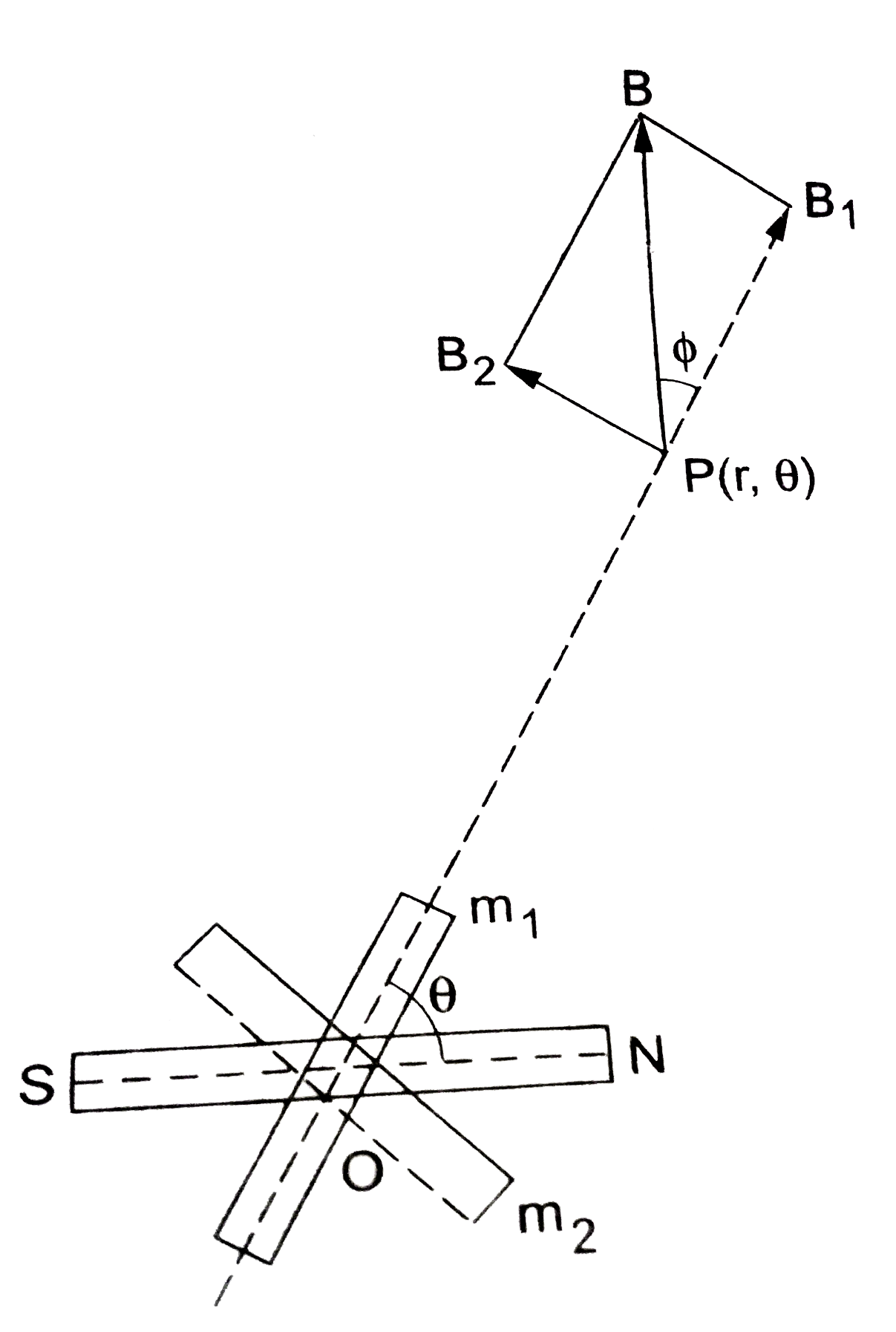
मान लिया चुंबकीय द्विध्रुव के केंद्र O के सापेक्ष किसी बिंदु P के ध्रुवीय नियामक (polar coordinates) (r, $θ$ ) हैं जहाँ पर चुंबकीय क्षेत्र $\vec{B}$ ज्ञात करना है । चुंबकीय आघूर्ण $\vec{m}$ को क्रमश: OP दिशा एवं इसके लंबवत दिशा में विघटित करने पर,
OP दिशा में घटक $m_{1} = m \cos θ$
तथा OP की लंबवत दिशा में घटक $m_{2} = m \sin θ$ .
अब $m_{1}$ के लिए बिंदु P अक्षीय स्थिति में है, अत: इसके कारण P पर चुंबकीय क्षेत्र
$B_{1} = \frac{μ_{0} \cdot 2 m_{1}}{4 π r^{3}} [समीकरण 1.21 से]$
या $B_{1} = \frac{μ_{0} 2 m \cos θ}{4 π r^{2}} ... .1 .35$
इसकी प्रकार, $m_{2}$ के लिए बिंदु P निरक्षीय स्थिति में है, अत: इसके कारण P पर चुंबकीय क्षेत्र
$B_{2} = \frac{μ_{0} m_{2}}{4 π r^{3}} [समीकरण 1.24 से]$
या $B_{2} = \frac{μ_{0} m \sin θ}{4 π r^{3}}$
अब $B_{1}$ एवं $B_{2}$ परस्पर लंबवत हैं, अत: P पर परिणामी चुंबकीय क्षेत्र $\vec{B}$ का परिमाण
$B = \sqrt{B_{1}^{2} + B_{2}^{2}} = \frac{μ_{0}}{4 π} \frac{m}{r^{3}} \sqrt{4 \cos^{2} θ + \sin^{2} θ}$
या $B = \frac{μ_{0}}{4 π} \frac{m}{r^{3}} \sqrt{1 + 3 \cos^{2} θ} ... .1 .36$
यदि परिणामी क्षेत्र $\vec{B}$ की दिशा OP रेखा के साथ $ϕ$ कोण बनाती हो, तो
$\tan ϕ = \frac{B_{2}}{B_{1}} = \frac{1}{2} \tan θ$
या $ϕ = \tan^{- 1} (\frac{1}{2} \tan θ) ... 1.37$
द्रष्टव्य: अक्षीय स्थिति में $θ = 0$ , अत: समीकरण 1.36 से, ${(B)}_{अक्षीय} = \frac{μ_{0}}{4 π} \frac{2 m}{r^{3}}$
इसी प्रकार, निरक्षीय स्थिति में $θ = 90^{\circ}$ , अत: ${(B)}_{निरक्षीय} = \frac{μ_{0}}{4 π} \frac{m}{r^{3}}$
अत: अनुपात $\frac{{(B)}_{अक्षीय}}{{(B)}_{निरक्षीय}} = \frac{2}{1}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

BHARATI BHAWAN-चुंबकीय क्षेत्र -लघु उत्तरीय प्रश्न

Home
Ask Doubt
Profile