विधुत-चुंबकीय तरंग की संचरण चाल c के लिए प्रमाणित करे : $c = \frac{1}{\sqrt{ε_{0} μ_{0}}},$ जहॉं $ε_{0} =$ निर्वात की परावैधुतता तथा a $μ_{0} =$ निर्वात की चुंबकशीलता।

Video Solution

Text Solution

Verified by Experts

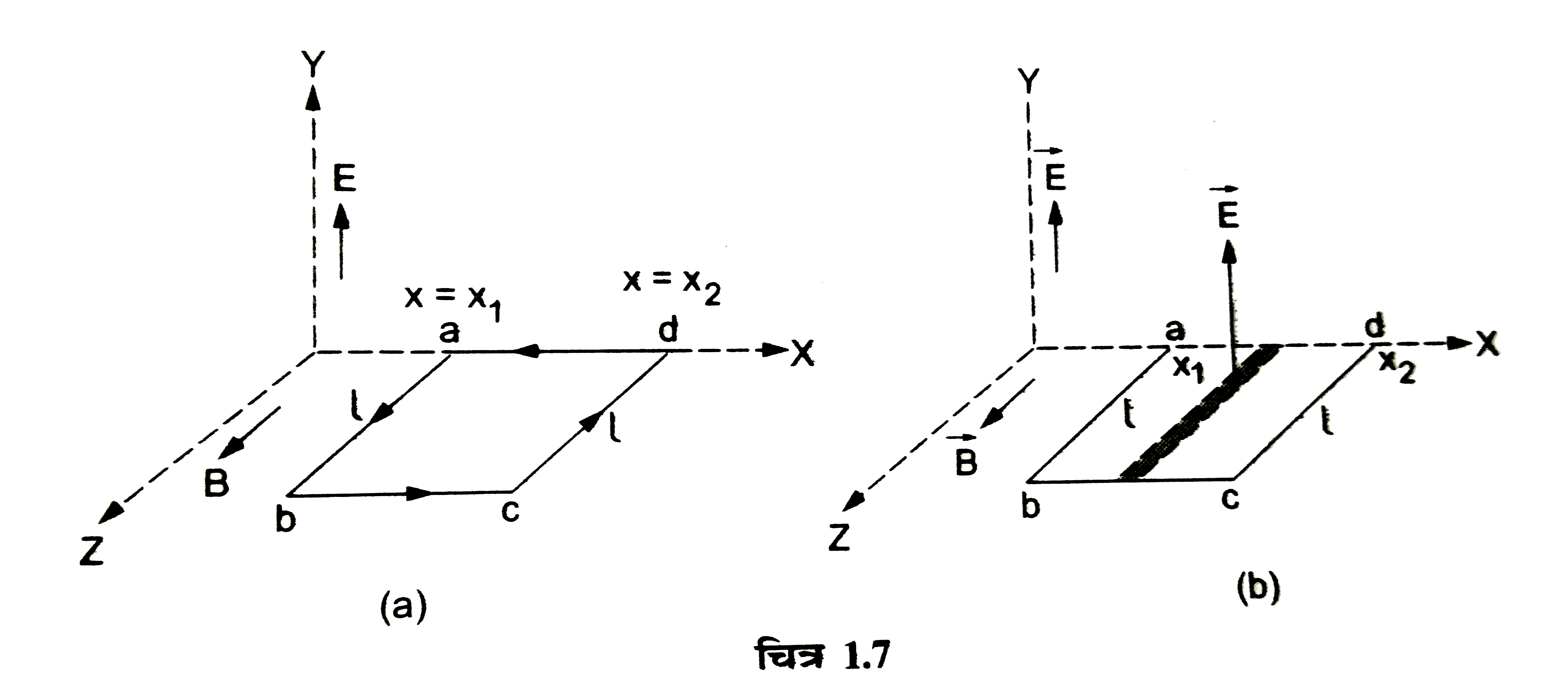
मान लिया की X -अक्ष के अनुदिश विधुत-चुंबकीय तरंग निर्वात में गमन कर रही है जिसके विधुत-क्षेत्र सदिश $\to E$ तथा चुंबकीय-क्षेत्र सदिश $\to B$ क्रमशः Y -तथा Z -दिशाओ के समांतर है (चित्र1.7) ।

मैक्सवेल द्वारा ऐम्पियर के संशोधित परिपथीय नियम में,
$\oint \to B \cdot d \to l = μ_{0} ε_{0} (I_{c} + I_{d}) = μ_{0} (0 + ε_{0} \frac{d ϕ_{E}}{d t})$
या $\oint \to B \cdot d \to l = μ_{0} \in_{0} \frac{d ϕ_{E}}{d t} \dots (1)$
समीकरण 1 के बाएं पक्ष का मान ज्ञात करने के लिए चित्र 1।7a में X -Z तल में खींचे गए आयताकार लूप abcd पर विचार करे। इसके लिए समाकलन
$\oint \to B \cdot d \to l = b \int a \to B \cdot d \to l + c \int b \to B \cdot d \to l + d \int b \to B \cdot d \to l + q \int d \to B \cdot d \to l$
$= B (x_{1}) l + 0 + [- B (x_{2})] l + 0$
$= B_{0} l [sin (ω t - k x_{1}) - sin (ω t - k x_{2}) \dots (2)$
अब समीकरण 1 के दाहिने पक्ष का मान ज्ञात करने के लिए चित्र ३३ (बी ) में दिखाए गए उसी आयताकार लूप में विधुत फ्लक्स $ϕ_{E}$ ज्ञात करने है।
$ϕ_{E} = \int d ϕ_{E} = x_{2} \int x_{1} \to E । d \to A = x_{2} \int x_{1} E d A cos 0$
$= x_{2} \int x_{1} E (x) l d x = E_{0} l x_{2} \int x_{1} sin (ω t - k x) d x$
$= E_{0} l [- cos (ω t - k x_{2}) - cos (ω t - k \cdot x_{1})] ।$
अब अवकलन करने पर,
$\frac{d ϕ_{E}}{d t} = \frac{E_{0} l}{k} [- ω sin (ω t - k x_{2}) + ω sin (ω t - k x_{1})]$
$= \frac{E_{0} l ω}{k} [sin (ω t - k x_{1}) - sin (ω t - k x_{2}) \dots (3)$
समीकरण 2 तथा 3 से प्राप्त मान समीकरण 1 में रखने पर,
$B_{0} l = μ_{0} \in_{0} \frac{E_{0} l ω}{k}$
या $\frac{B_{0}}{E_{0}} = μ_{0} \in_{0} \frac{ω}{k} = μ_{0} \in_{0} \frac{2 π f}{2 π / λ} = μ_{0} \in_{0} λ f = μ_{0} λ f = μ_{0} \in_{0} c$
लेकिन, (B_(0))/(E_(0))=1/c $< b r >$ therefore1/c=mu_(0)in _(0)c $< b r > य ा$ c^(2)=(1)/(mu_(0)in_(0)) $< b r >$ thereforec=(1)/(sqrt(mu_(0)in_(0))) $< b r > म ै क ् स व े ल द ् व ा र ा$ mu_(0) $त थ ा$ in_(0) $क े म ा न र क न े प र प ् र ा प ् त म ा न$ 3xx10^(8)ms^(-1) आता है जो निर्वात में प्रकाश का वेग है। इसी आधार पर मैक्सवेल ने यह संकेत दिया कि प्रकाश भी विधुत-चुंबकीय तरंग है ।]

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROMAGNETIC WAVES

Topper's Solved these Questions

Similar Questions

BHARATI BHAWAN-विधुत-चुंबकीय तरंगे -प्रश्नावली (लघु उत्तरीय प्रश्न)

Home
Ask Doubt
Profile