अपवर्तनांक μ वाले एक अपवर्तक सतह पर प्रकाश की एक किरण आपतित होती है। यदि प्रथम और द्वितीय फोकस-दूरियाँ f1 तथा f2 हो, तो सिद्ध करे की f2+μf1=0
अपवर्तनांक μ के गोलीय सतह से अपवर्तन के सूत्र से, μv−1u=μ−1R प्रथम फोकस-दुरी f1 के लिए प्रतिबिंब अनंत पर बनता है, अतः u=f1 तथा v=∞
∴μ∞−1f1=μ−1R या −1f1=μ−1R ...(i)
फिर, द्वितीय फोकस-दुरी f2 के लिए वस्तु अनंत पर होती है और प्रतिबिंब द्वितीय फोकस पर बनता है, अतः u=∞ तथा v=f2
∴μf2−1∞=μ−1R या μf2=μ−1R ...(ii)
समीकरण (i) और (ii) से, −1f1=μf2 या f2=−μf1 या f2+μf1=0
Topper's Solved these Questions
- गोलीय सतहों से प्रकाश का अपवर्तन BOOK - BHARATI BHAWANCHAPTER - गोलीय सतहों से प्रकाश का अपवर्तन EXERCISE - प्रश्नावली (दीर्घ उत्तरीय प्रश्न )
8 Videos
- गोलीय सतहों से प्रकाश का अपवर्तन BOOK - BHARATI BHAWANCHAPTER - गोलीय सतहों से प्रकाश का अपवर्तन EXERCISE - आंकिक प्रश्न
9 Videos
- गोलीय सतहों से प्रकाश का अपवर्तन BOOK - BHARATI BHAWANCHAPTER - गोलीय सतहों से प्रकाश का अपवर्तन EXERCISE - प्रश्नावली (अतिलघु उत्तरीय प्रश्न)
7 Videos
- गोलीय सतहों से प्रकाश का अपवर्तन BOOK - BHARATI BHAWANCHAPTER - गोलीय सतहों से प्रकाश का अपवर्तन EXERCISE - उदाहरण
14 Videos
- चुंबकीय क्षेत्र BOOK - BHARATI BHAWANCHAPTER - चुंबकीय क्षेत्र EXERCISE - उदाहरण
12 Videos
Similar Questions
किसी गोलीय सतह से अपवर्तन के लिए सूत्र μ2v−μ1u=μ2−μ1r निकालें।
View Solution6 cm त्रिज्या तथा 1.5 अपवर्तनांक वाले एक काँच के गोले में हवा का एक छोटा बुलबुला, यदि इसमें से होकर गुजरनेवाले व्यास की और से देखा जाए, तो पास वाली सतह से 2 cm पर मालूम पड़ता है। बुलबुले की वास्तविक स्थिति ज्ञात करे।
View Solutionलेंस की क्षमता की परिभाषा दे। इसका SI मात्रक क्या है?
View Solutionवायु में रखे 5 cm त्रिज्या के काँच (अपवर्तन 1.50 ) के गोले (sphere) के अंदर वायु का एक छोटा बुलबुला (bubble ) है | बुलबुले से होकर खींचे गए व्यास के अनुरेख (along ) देखने पर बुलबुला निकट सतह (near surface ) से 2.5 cm पर प्रतीत होता है | इसका स्थान क्या है ?
View Solutionएक छोटे छड़ चुंबक का अक्ष 0.25T के एकसमान चुम्बकीय क्षेत्र के साथ 30∘ कोण पर विक्षेपित रहने पर 4.5×10−2j के बल -आघूर्ण का अनुभव करता है । चुंबक के चुंबकीय आघूर्ण (magnetic mement) का परिमाण ज्ञात करें।
View SolutionIf F1andF2 aare two vectors of equal magniudes F such that |F1.F2|=|F1×F2|,then|F1+F2| equals to
View SolutionFor the following table, the values of f1, f0 and f2 are respectively______.
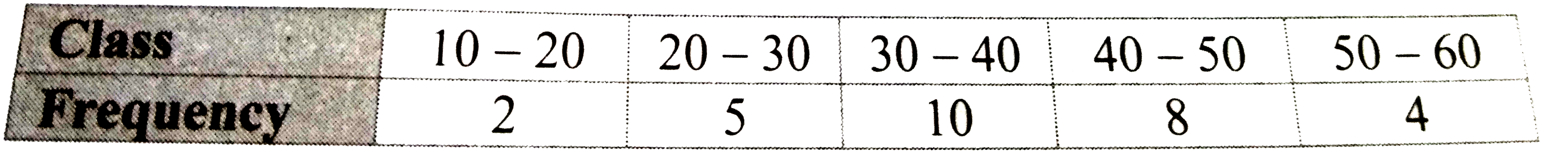
View SolutionGiven F1=1,F2=3andFn=Fn−1+Fn−2 then F5 is
View SolutionGiven F1=1,F2=3andFn=Fn−1+Fn−2 then F3 is ____.
View Solutionl+(f1−f02f1−f0−f2)×hसूत्र है:
View Solutionबहुलक =l+(f1−f02f1−f0−f2)×h में h होता है ।
View Solutionदो सदिशों F1 व F2 का परिमाण समान है जिसका मान F है। यदि |F1⋅F2|=|F1×F2| तब |F1+F2| बराबर है
View SolutionTwo spring force constant K_(1)" तथा K_(2) is. If both force F_(1)" तथा F_(2) is, (F_(1))/(F_(2)) Find out
View SolutionSupposed that f_(1):RtoR,f_(2):[0,oo)toR,f_(3):RtoR And f_(4):rto[0,oo) As follows f_(1)(x)={((|x),यदि,xlt0),(e^(x),यदि,xge0):} f_(2)(x)=x^(2) f_(3)(x)={(sinx, यदि,xlt0),(x, यदि,xge0):} And f_(a)(x)={(f_(2)(f_(1)(x)),यदि,xlt0),(f_(2)(f_(1)(x))-1,यदि ,xge0):}
View SolutionF(x) को दो वास्तविक फलनों f1(x),x∈IR, तथा f2(x)={sin1xयदिx≠00यदिx=0
के गुणनफल के रूप में निम्न प्रकार | 0, यदि x = 0 है से परिभाषित कीजिये F(x)={f1(x)f2(x)यदिx≠00यदिx=0
कथन-1: Fx, IR पर सतत् है।
कथन-2 : f1(x) तथा f2(x) , IR पर सतत् है।
View Solution
