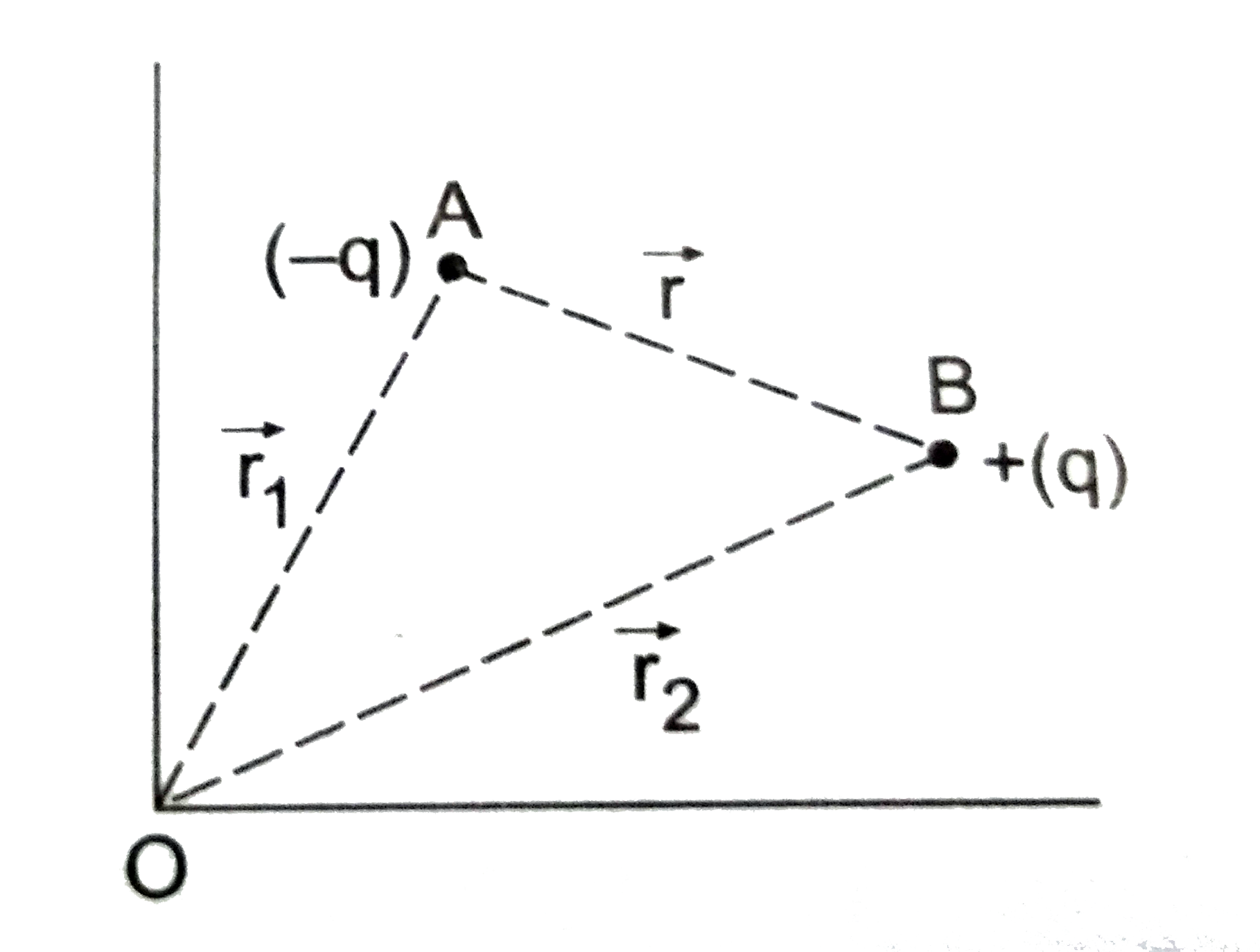
किसी विद्युत व्दिध्रुव का नेट आवेश शून्य होता हैं , लेकिन इसका व्दिध्रुव - आपूर्ण अशून्य होता हैं । बिंदु A तथा B पर स्थित (-q) तथा (+ q) आवेश के सरल निकाय के लिए चित्र से (−q)→r1+(+q)→r2=q(→r2−→r1)=q→r=→P = व्दिध्रुव - आघूर्ण सदिश । व्यापक रुप से यदि आवेश के वितरण में नेट आवेश शून्य हो , तो उस निकाय का व्दिध्रुव - आघूर्ण सदिश रुप से परिभाषित होता हैं :
आवेश के असंतत (discrete) वितरण के लिए , →P=∑−−→riqi तथा आवेश के संतत ( continuous) वितरण के लिए , →P=∫→ridqi
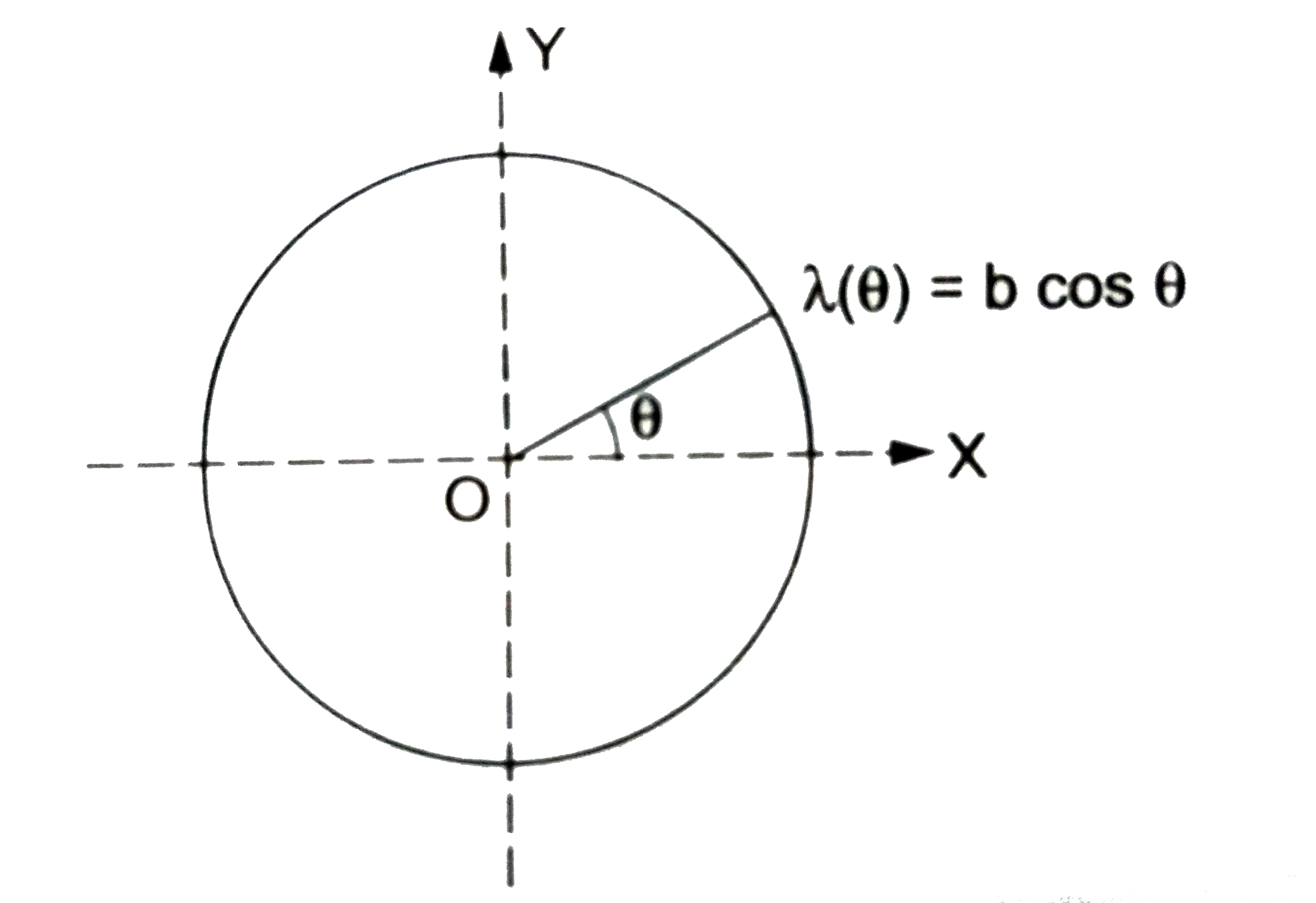
XY - तल में स्थित त्रिज्या R के एक आवेशित रिंग का केंद्र - मूलबिंदु o पर स्थित हैं तथा इसके आवेश का रैखिक घनत्व λ, कोण θ के फलन के रुप में संबंध λ(θ)=bcosθ से व्यक्त होता हैं । आवेशित रिंग का विद्युत व्दिध्रुव - आघूर्ण हैं
πbR2ˆi
πbR2ˆj
2πbR2ˆi
2πbR2ˆj
The correct Answer is:A
कोण θ की दिशा में अल्पांश (Rdθ ) पर आवेश .
अतः , परिभाषा से ,
→P=∫→rdq=∫20(π)(Rcosθˆi+Rsinθˆj)Rbcosθ.dθ ,
=bR2∫20(π)(cos2θ⋅ˆi+sinθcosθ⋅J)dθ=(π)bR2ˆi.]
Topper's Solved these Questions
Similar Questions
केथोड किरणों के लिए निम्नांकित में क्या सत्य है?
View Solutionकॉलम A में दी गई भौतिक राशियों को कॉलम B में व्यक्ति उनके संगत SI मात्रक के बीच मेल स्थापित करे ।
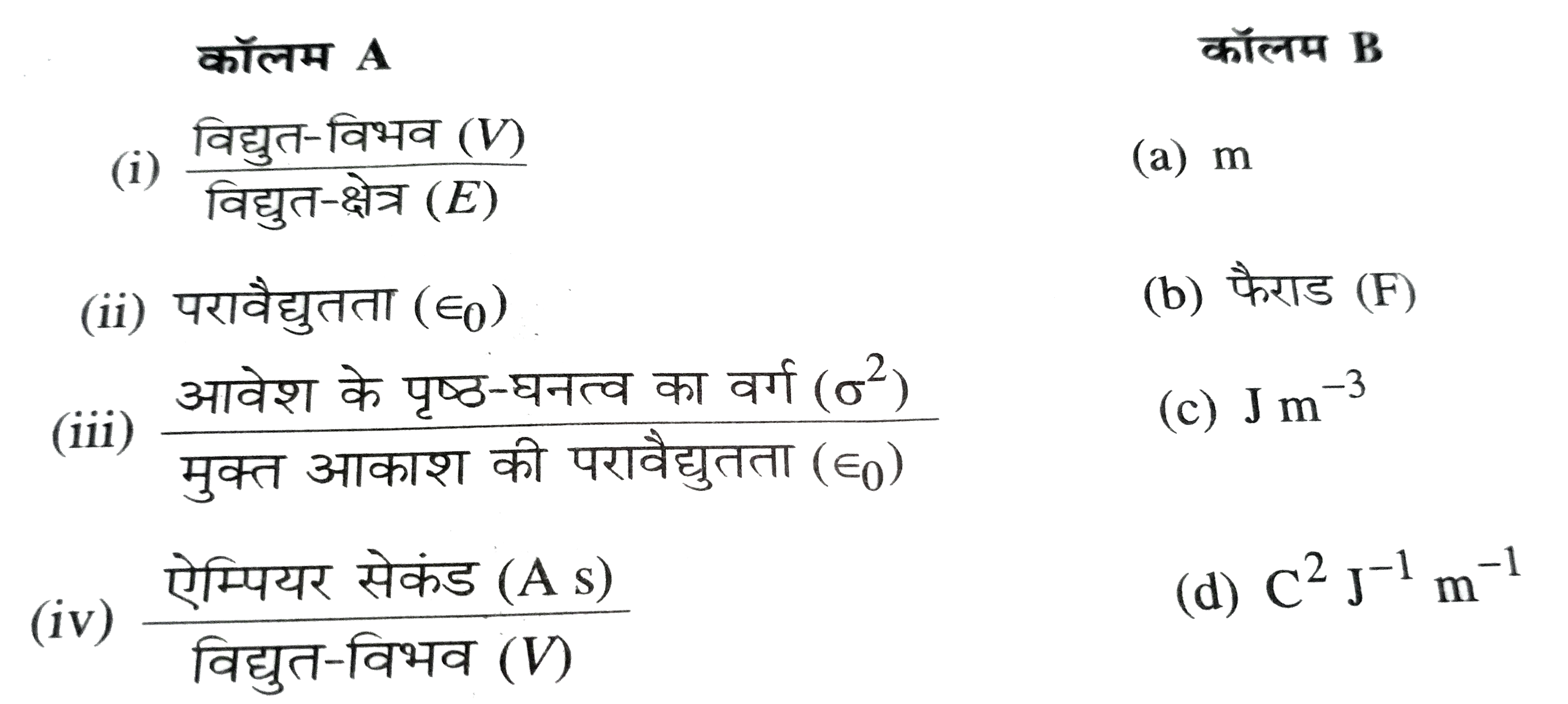
View SolutionIf →r1,→r2,→r3 are the position vectors of the collinear points and scalar pandq exist such that →r3=p→r1+q→r2, then show that p+q=1.
View Solution→p,→q,and→r are three mutually perpendicular vectors of the same magnitude. If vector →x satisfies the equation →p×((→x−→q)×→p)+→q×((→x−→r)×→q)+→r×((→x−→p)×→r)=0,then→x is given by a.12(→p+→q−2→r) b. 12(→p+→q+→r) c. 13(→p+→q+→r) d. 13(2→p+→q−→r)
View SolutionThree vectors vec(P) , vec(Q) and vec( R) are such that |vec(P)| , |vec(Q )|, |vec(R )| = sqrt(2) |vec(P)| and vec(P) + vec(Q) + vec(R ) = 0 . The angle between vec(P) and vec(Q) , vec(Q) and vec(R ) and vec(P) and vec(R ) are
View SolutionLet vec(p),vec(q),vec(r) be three unit vectors such that vec(p)xxvec(q)=vec(r) . If vec(a) is any vector such that [vec(a)vec(q)vec(r )]=1,[vec(a)vec(r)vec(p )]=2 , and [vec(a)vec(p)vec(q )]=3 , then vec(a)=
View SolutionColumn- IColumn II(Operation of nonzero vectors→Pand→Q)(Possivle angle between→Pand→Q)(A)∣∣→P×→Q∣∣=0(P) 90∘(B)∣∣→P×→Q∣∣=√3→P.→Q(Q) 180∘(C)→P+→Q=→RandP+Q=R(R) 60∘(D)∣∣→P+→Q∣∣=∣∣→P−→Q∣∣(S) 0∘(T) 30∘
View Solutionकिसी विद्युत व्दिध्रुव का नेट आवेश शून्य होता हैं , लेकिन इसका व्दिध्रुव - आपूर्ण अशून्य होता हैं । बिंदु A तथा B पर स्थित (-q) तथा (+ q) आवेश के सरल निकाय के लिए चित्र से (−q)→r1+(+q)→r2=q(→r2−→r1)=q→r=→P = व्दिध्रुव - आघूर्ण सदिश । व्यापक रुप से यदि आवेश के वितरण में नेट आवेश शून्य हो , तो उस निकाय का व्दिध्रुव - आघूर्ण सदिश रुप से परिभाषित होता हैं :
आवेश के असंतत (discrete) वितरण के लिए , →P=∑−−→riqiतथाआवेशकेसंतत(cont∈uous)वितरणकेलिए,vec(P) = int vec(r_(i))dq_(i).<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/SMA_HIN_PHY_XII_P2_U8_C04_E01_010_Q01.pngwh=80%mx-autosty≤=background:white;><br>तीनआवेशोंसेबनेकिसीनिकायकाव्दिध्रुम−आघूर्णज्ञातकरेंजिसमेंआवेश1 mu Cकीस्थिति(3Å,0,0),आवेश2 mu Cकीस्थिति(0,2Å,0)तथा - 3mu C आवेश की स्थिति (0,0 , -1 Å) पर हो ।
View Solutionकिसी विद्युत व्दिध्रुव का नेट आवेश शून्य होता हैं , लेकिन इसका व्दिध्रुव - आपूर्ण अशून्य होता हैं । बिंदु A तथा B पर स्थित (-q) तथा (+ q) आवेश के सरल निकाय के लिए चित्र से (−q)→r1+(+q)→r2=q(→r2−→r1)=q→r=→P = व्दिध्रुव - आघूर्ण सदिश । व्यापक रुप से यदि आवेश के वितरण में नेट आवेश शून्य हो , तो उस निकाय का व्दिध्रुव - आघूर्ण सदिश रुप से परिभाषित होता हैं :
आवेश के असंतत (discrete) वितरण के लिए , →P=∑−−→riqi तथा आवेश के संतत ( continuous) वितरण के लिए , →P=∫→ridqi.
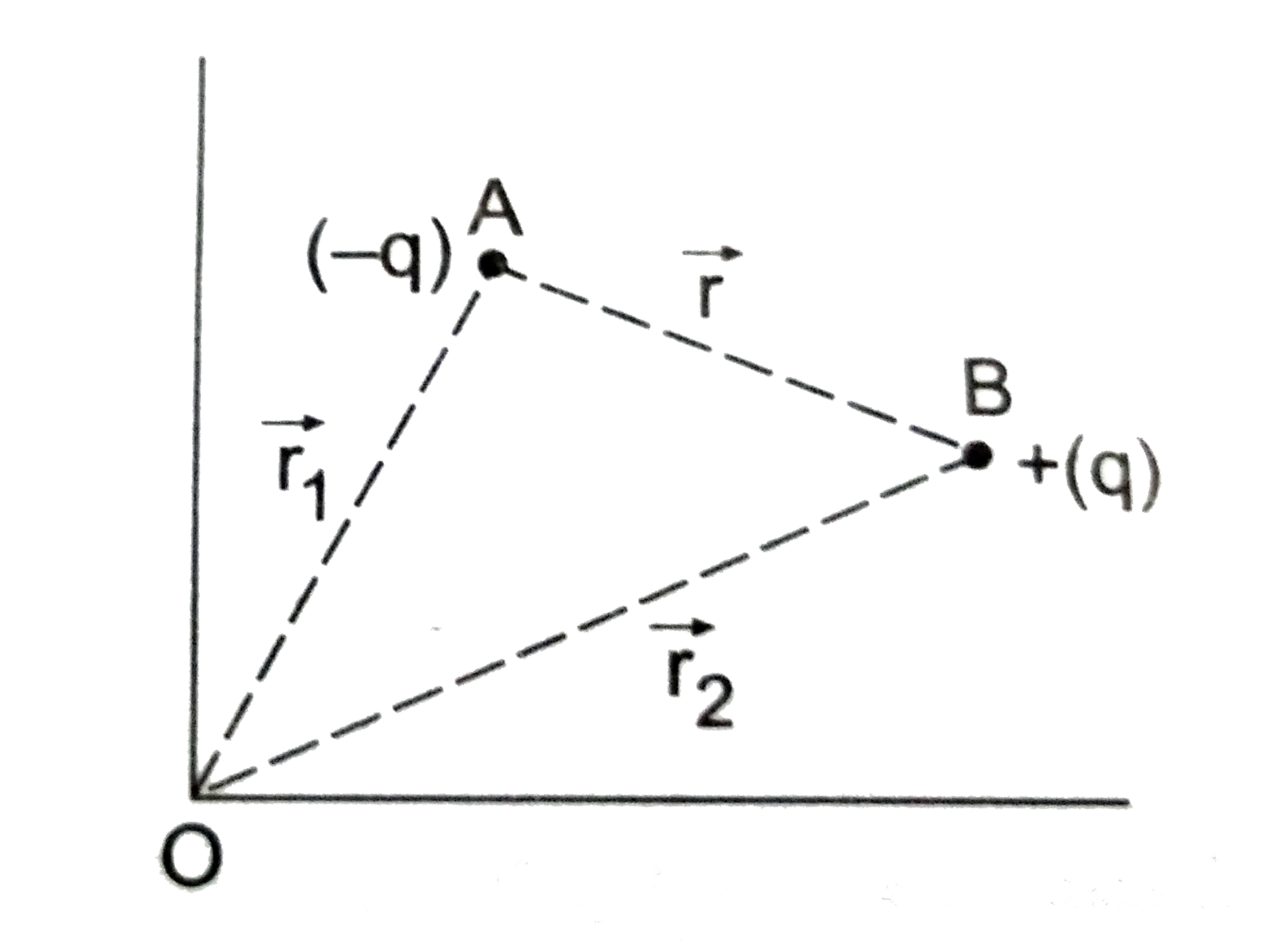
उपर्युक्त आवेशित रिंग के कारण बिंदु P(nR, 0,0) पर विद्युत - क्षेत्र ज्ञात करें , जहाँ n का मान बहूत बड़ा हैं ।
View Solutionसदिश →b के समान्तररेखा के समतल →r.→n=q के बीच का कोण है -
View SolutionGiven that →a,→b,→p,→q are four vectors such that →a+→b=μ→p,→b⋅→q=0and∣∣→b∣∣2=1,whereμ is a scalar. Then ∣∣(→a.→q)→p−(→p.→q)→a∣∣ is equal to (a) 2|→p.→q| (b) (1/2)|→p.→q| (c) |→p×→q| (d) |→p.→q|
View SolutionIf vec P+ vec Q = vec R and |vec P| = |vec Q| = | vec R| , then angle between vec P and vec Q is
View SolutionThree vectors vec(P), vec(Q), vec(R) obey vec(P) + vec(Q) = vec(R) and P^(2) + Q^(2) = R^(2) the angle between vec(P) & vec(Q) is
View SolutionGiven that vec a , vec b , vec p , vec q are four vectors such that vec a+ vec b=mu vec p , vec b*vec q=0a n d|vec b|^2=1,w h e r emu is a scalar. Then |( vec adot vec q) vec p-( vec pdot vec q) vec a| is equal to (a) 2| vec p . vec q| (b) (1//2)| vec p . vec q| (c) | vec pxx vec q| (d) | vec p . vec q|
View Solutionविभिन्न आवेश वितरण के कारण विद्युत क्षेत्र तीव्रता - आवेश का वितरण|बिंदु आवेश|रेखिया आवेश|वलय के केन्द्रो अवाम अक्ष पर|विद्युत् क्षेत्र में आवेशित कण|OMR
View Solution
