मैक्सवेल व्दारा प्रतिपादित क्षेत्र - समीकरणों (field equations) के आधार पर विद्युत - चुंबकीय तरंग की उत्पत्ति , संचरण तथा अन्य घटनाओं की व्याख्या की जाती हैं । इस सिध्दांत के अनुसार , विद्युत क्षेत्र →E तथा चुंबकीय क्षेत्र →B एक - दूसरे से अतंरबध्द है तथा तरंग संचरण के क्रम में दोनों क्षेत्र समय के साथ परिवर्ती होते हैं । मुक्त आकाश में वे प्रकाश की चाल (c0=3×108ms−1) से गमन करती हैं । मैक्सवेल के चार समीकरण मूलतः (i) चुंबकत्व गॉस का नियम , (ii) स्थिर वैद्युतिकी में गॉस का नियम , (iii) फैराडे का विद्युत - चुंबकीय प्रेरण का नियम तथा
(iv) ऐम्पियर के नियम का एक पूर्ण सेट हैं ।
चालन धारा (Ic) तथा विस्थापन धारा (Id=ε0dϕEdt) के पद में ऐम्पियर का नियम जिस समीकरण से व्यक्त होता हैं , वह हैं
∮→B⋅d→l=μ0(Ic+Id)
∮→E⋅d→l=μ0(Ic+Id)
∮→B⋅d→l=∈0(Ic+Id)
∮→E⋅d→l=∈0(Ic+Id)
The correct Answer is:A
Step by step video, text & image solution for मैक्सवेल व्दारा प्रतिपादित क्षेत्र - समीकरणों (field equations) के आधार पर विद्युत - चुंबकीय तरंग की उत्पत्ति , संचरण तथा अन्य घटनाओं की व्याख्या की जाती हैं । इस सिध्दांत के अनुसार , विद्युत क्षेत्र vec(E) तथा चुंबकीय क्षेत्र vec(B) एक - दूसरे से अतंरबध्द है तथा तरंग संचरण के क्रम में दोनों क्षेत्र समय के साथ परिवर्ती होते हैं । मुक्त आकाश में वे प्रकाश की चाल (c_(0) = 3xx10^(8)m s^(-1) ) से गमन करती हैं । मैक्सवेल के चार समीकरण मूलतः (i) चुंबकत्व गॉस का नियम , (ii) स्थिर वैद्युतिकी में गॉस का नियम , (iii) फैराडे का विद्युत - चुंबकीय प्रेरण का नियम तथा (iv) ऐम्पियर के नियम का एक पूर्ण सेट हैं । चालन धारा (I _(c)) तथा विस्थापन धारा ( I_(d) = epsi_(0) (d phi_(E))/(dt)) के पद में ऐम्पियर का नियम जिस समीकरण से व्यक्त होता हैं , वह हैं by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
केथोड किरणों के लिए निम्नांकित में क्या सत्य है?
View Solutionकॉलम A में दी गई भौतिक राशियों को कॉलम B में व्यक्ति उनके संगत SI मात्रक के बीच मेल स्थापित करे ।
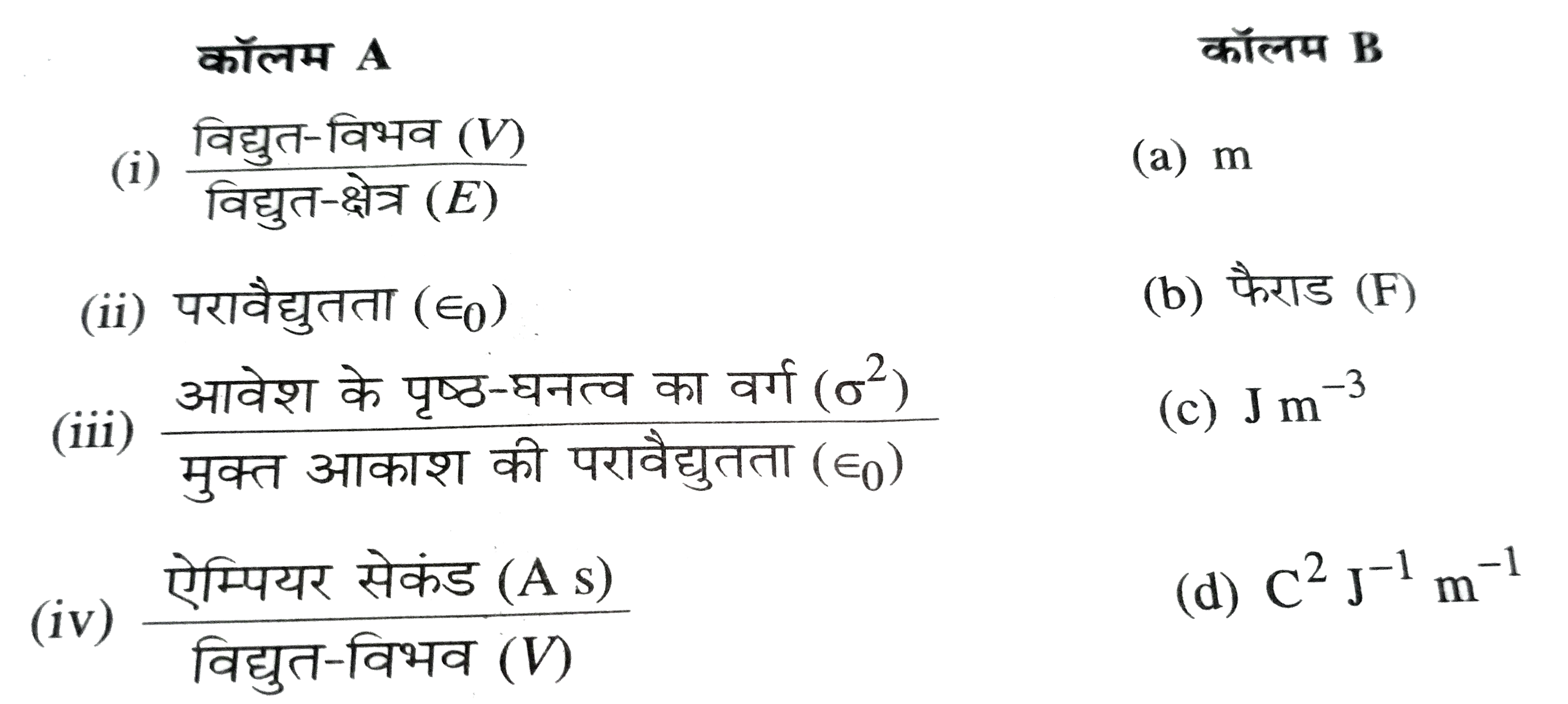
View Solutionआवेशित वलय के कारण विद्युत क्षेत्र की तीव्रता
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionचुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता | एक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष तथा केन्द्र पर चुंबकीय क्षेत्र | ऐम्पियर का परिपथीय नियम
View Solutionचुंबकीय क्षेत्र में आवेशित कण की गति
View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के केन्द्र पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionगतिमान आवेश की चुंबकीय क्षेत्र में गति
View Solutionपरिवर्तित चुंबकीय क्षेत्र तथा प्रेरित विद्युत क्षेत्र
View Solutionपरिवर्ती चुंबकीय क्षेत्र तथा प्रेरित विद्धुत क्षेत्र
View Solutionविद्युत तथा चुंबकीय क्षेत्र मे आवेश की गति
View Solutionकूलॉम के नियम पर महत्वपूर्ण उदाहरण |विद्युत क्षेत्र |विद्युत क्षेत्र की दिशा |विद्युत बल एवं विद्युत क्षेत्र मे संबंध | विद्युत क्षेत्र का अध्यारोपण |OMR|Summary
View Solution
