मान लीजिये f:R→R में एक अवकलनीय फलन है जो प्रतिबन्ध को सन्तुष्ट करता है
f.(x+y3)=2+f(x)+f(y)3,∀x,y∈Rतथा f'(2)=2
यदि g(x)=|f(|x|)−3|,Ax∈R हो, तो g(x) के लिए
केवल एक अवकलनीय बिन्दु है
दी अवकलनीय बिन्दु हैं
तीन अवकलनीय हैं
चार अवकलनीय बिन्दु हैं
The correct Answer is:C
चूँकि f'(x)=limh→0f(x+h)−f(x)h
=limh→0f(3x+3h3)−f(3x+03)h
=limh→02+f(3x)+f(3h)3−2+f(3x)+f(0)3h
=limh→0f(3h)−f(0)3h−0=f'(0)
⇒f'(2)=f'(0)=2 [∵f'(2)=2]
⇒r'(x)=2
⇒f(x)=2x+c ( समाकलन करने पर ) ...(i)
f(x+y3)=2+f(x)+f(y)3में x=y=0
रखने पर, ⇒f(0)=2 अब समी (i) से, f(0)=0+c=2⇒c=2
समी (i) से, f(x)=2x+2
चूँकि f(|x|)=2|x|+2
∴f(|x|)−3=2|x|−1
तथा g(x)=|f(|x|−3)|=|2|x|−1|
अब, y=2x−1 का ग्राफ निम्न है
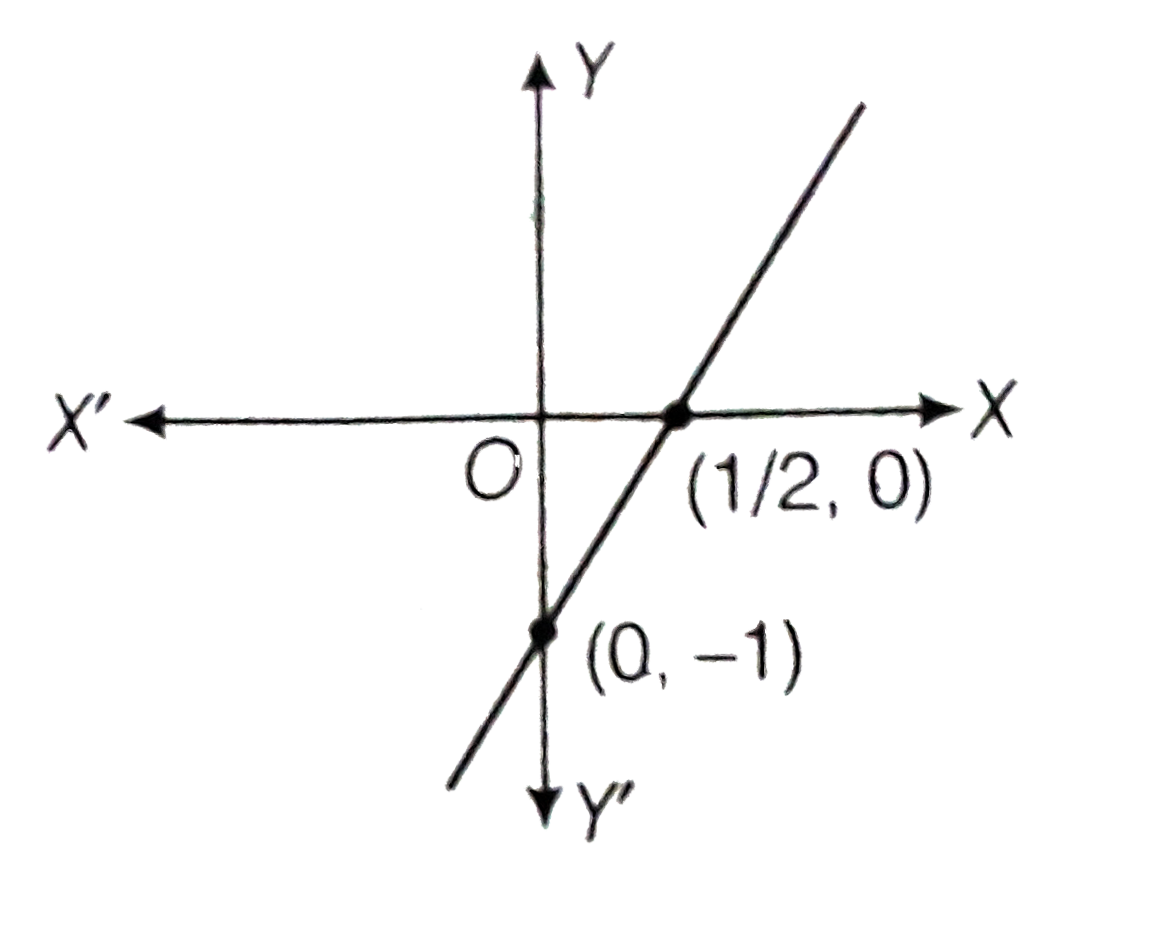
तथा y=2|x|−1 का ग्राफ निम्न है
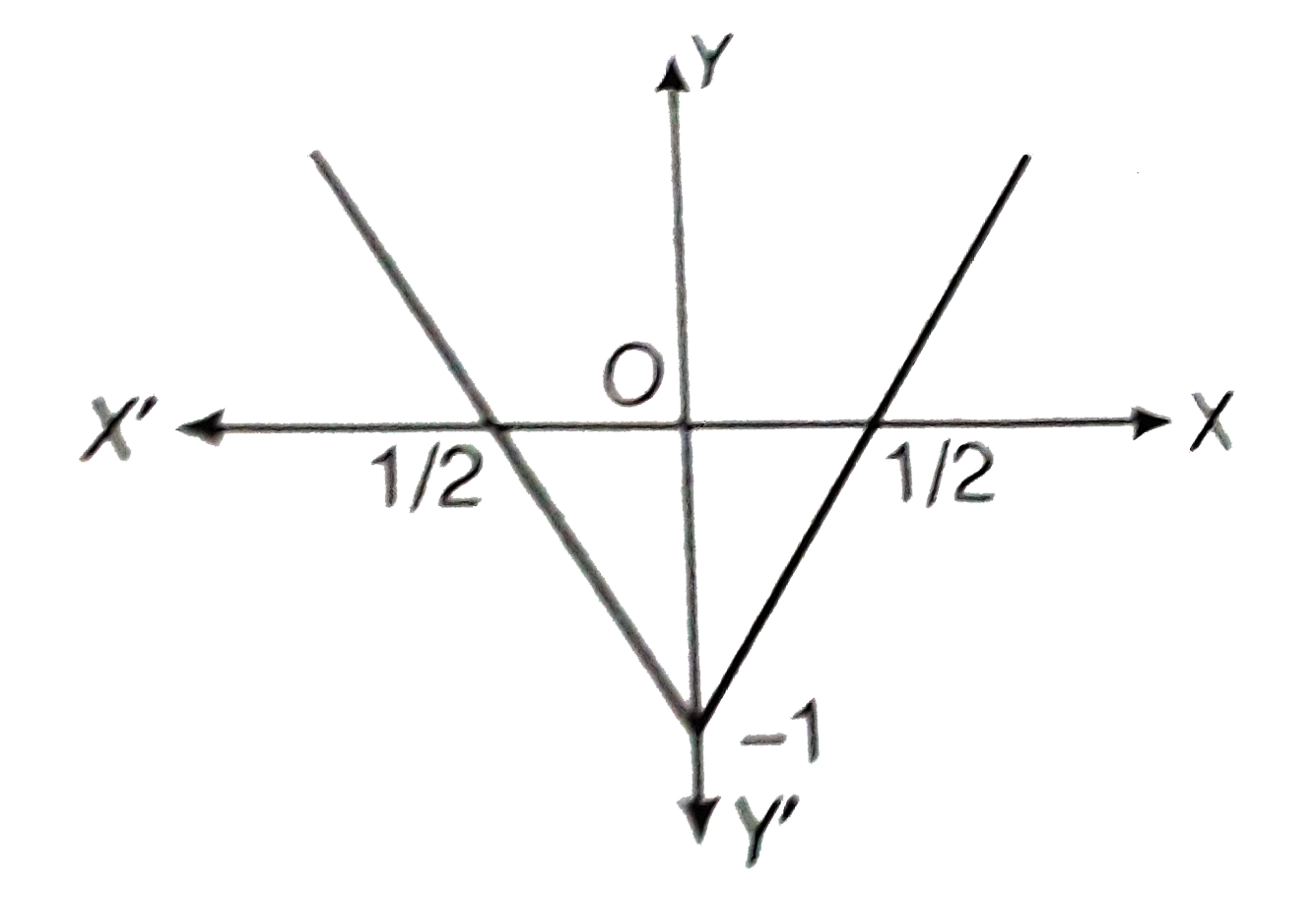
तथा g(x)=|2|x|−1| का ग्राफ निम्न है
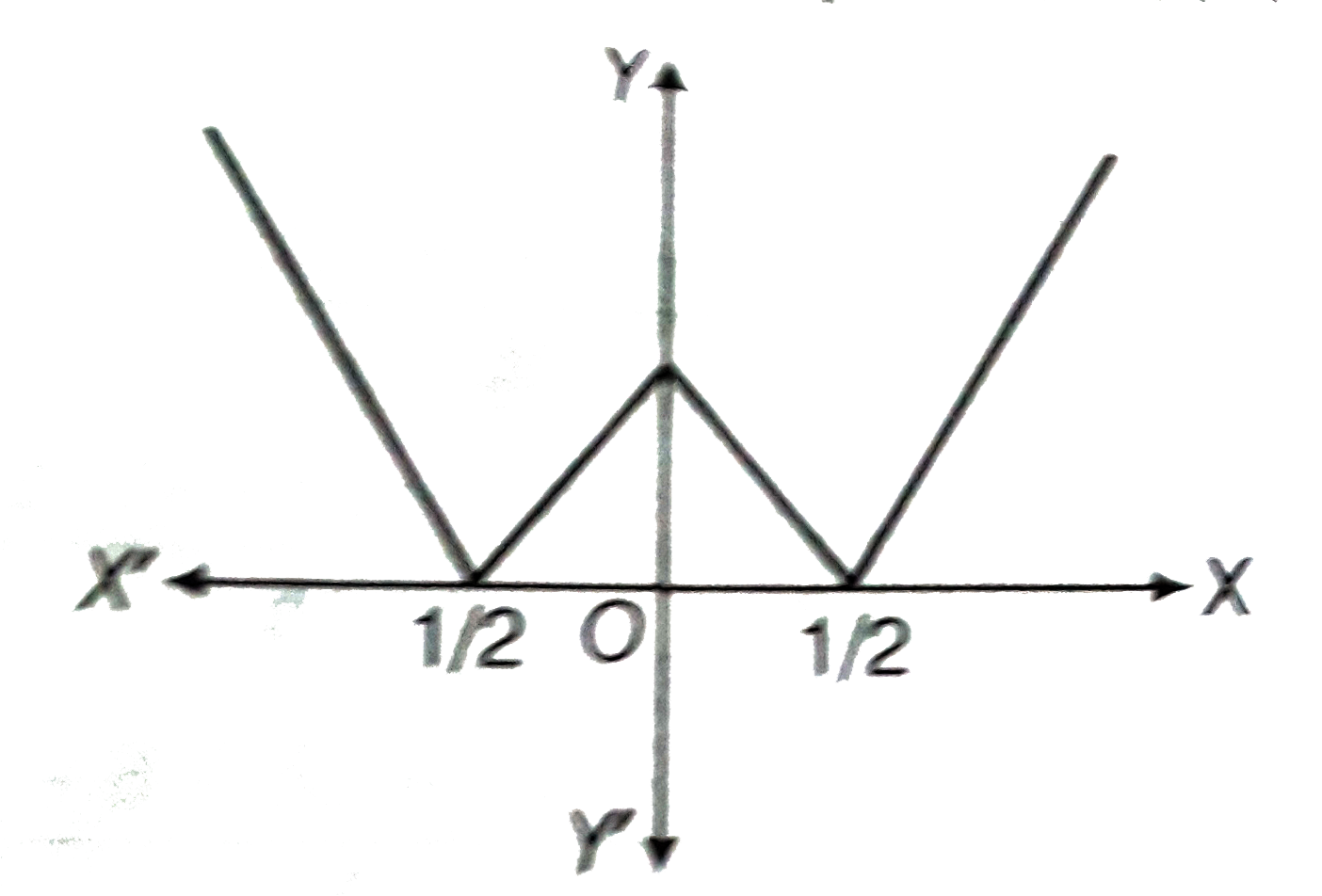
∴ बिन्दुओं की संख्या जहाँ फलन अवकलनीय नहीं है, 3 है ।
Topper's Solved these Questions
Similar Questions
यदि limx→0kxcosecx=limx→0xcoseckx है, तो k का मान है
05:54View Solution∣∣ ∣ ∣∣−a2abacab−b2bcacbc−c2∣∣ ∣ ∣∣ किसके बराबर है ?
14:27View SolutionConsider f:R+→Rsuch thatf(3)=1 for a∈R+andf(x).f(y)+f(3x)f(3y)=2f(xy)∀x,y∈R+. Then find f(x).
04:02View SolutionLet f:[-(1)/(2),2]rarr R and g:[-(1)/(2),2]rarr R be functions defined by f(x)=[x^(2)-3] and g(x)=|x|f(x)+|4x-7|f(x), where [y] denotes the greatest integer less than or equal to y for y in R. Then,
View SolutionLet f:R→R be a function such that
f(x+y)=f(x)+f(y),Aax,y∈R. If f (x) is differentiable at x = 0, then05:48View Solutionमान लीजिये f(x) एक फलन है जो f(x+y)=f(x)+f(y) और f(x)=x2g(x) को सन्तुष्ट करता है ∀x,y∈R जहाँ g(x) सतत फलन है तो -
01:56View Solutionमान लीजिये f:R→R में एक अवकलनीय फलन है जो प्रतिबन्ध को सन्तुष्ट करता है
f.(x+y3)=2+f(x)+f(y)3,∀x,y∈Rतथा f'(2)=2
f(1) का मान होगा02:07View Solutionयदि f:R→R तथा g:R→R निम्न प्रकार परिभाषित हैं कि f(x) = 2x - 3 तथा g(x)=x2+5 , तो g(g(x)) ज्ञात कीजिए |
04:40View Solutionयदि f:R→R तथा g:R→R , जहां f(x) = 2x +3 तथा g(x)=x2+1 तब (gof)(2) का मान है
13:09View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
03:45View Solutionमाना कि फलन f:[−12,2]→R तथा g:[−12,2]→R,f(x)=[x2−3] और g(x)=|x| f(x) +|4x-7|f(x) से परिभाषित है, जहाँ y∈R के लिए y से कम या y के बराबर के महत्तम पूर्णाक (greatest integer less than or equal toy) को [v] द्वारा दर्शाया गया है। तब
04:50View Solutionएक द्विघात बहुपद f(x), जो f(0)=0,f(1)=1,f'(x)>0, को सभी x∈(0,1) के लिए संतुष्ट करता है, है
01:07View Solutionएक फलन g जो प्रत्येक वास्तविक संख्या x>0 के लिए परिभाषित है तथा g(1)=1,g'(x2)=x3 को सभी x>0 के लिए सन्तुष्ट करता है, तो g (4) का मान है
00:52View SolutionThe function f:R+→R+,f(x)=x3,g:R+→R+,g(x)=x13 then (fog)(x) = .........
04:01View SolutionIf f:R→R,f(x)=x−2,g:R→R,g(x)=x+2 then (f+g)(x)= ……..
15:12View Solution

