Question

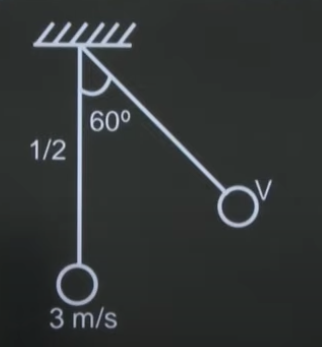
A pendulum bob has a speed 3m/s while passing thorugh its lowest position. What is its speed when it makes an angle of ${60}^0$ with the vertical? The length of the pendulum is 0.5m Take $g=10\frac{m}{s^2}$.

Explanation

To solve the problem, we will use the principle of conservation of mechanical energy. The total mechanical energy of the pendulum bob remains constant as it swings, assuming there are no non-conservative forces acting on it (like air resistance or friction).

1. Identify Initial and Final States:
- Initial state (lowest position): Speed \( v_1 = 3 \, \text{m/s} \)
- Final state (at \( 60^\circ \) with the vertical): Speed \( v_2 \) (unknown)

2. Determine the Length of the Pendulum:
- Given length \( l = 0.5 \, \text{m} \)

3. Calculate Initial Kinetic Energy (KE):
\( KE_1 = \frac{1}{2} m v_1^2 = \frac{1}{2} m (3)^2 = \frac{9}{2} m \)

4. Calculate Initial Potential Energy (PE):
- At the lowest position, the height \( h_1 = 0 \), hence:
\( PE_1 = mgh_1 = mg(0) = 0 \)

5. Total Mechanical Energy at the Lowest Position:
\( E_1 = KE_1 + PE_1 = \frac{9}{2} m + 0 = \frac{9}{2} m \)

6. Calculate Final Potential Energy (PE) at \( 60^\circ \):
- The height \( h_2 \) when the pendulum makes an angle of \( 60^\circ \) can be calculated using:
\( h_2 = l - l \cos(60^\circ) = l(1 - \cos(60^\circ)) = 0.5(1 - 0.5) = 0.5 \times 0.5 = 0.25 \, \text{m} \)
- Therefore, the final potential energy is:
\( PE_2 = mgh_2 = mg(0.25) \)

7. Calculate Final Kinetic Energy (KE):
- The total mechanical energy at this position is:
\( E_2 = KE_2 + PE_2 \)
- Since energy is conserved, \( E_1 = E_2 \):
\( \frac{9}{2} m = KE_2 + mg(0.25) \)

8. Express KE in terms of \( v_2 \):
\( KE_2 = \frac{1}{2} m v_2^2 \)
- Substitute into the energy conservation equation:
\( \frac{9}{2} m = \frac{1}{2} m v_2^2 + mg(0.25) \)

9. Cancel \( m \) from the equation:
\( \frac{9}{2} = \frac{1}{2} v_2^2 + g(0.25) \)

10. Substitute \( g = 10 \, \text{m/s}^2 \):
\( \frac{9}{2} = \frac{1}{2} v_2^2 + 10(0.25) \)
\( \frac{9}{2} = \frac{1}{2} v_2^2 + 2.5 \)

11. Simplify the equation:
\( \frac{9}{2} - 2.5 = \frac{1}{2} v_2^2 \)
\( \frac{9}{2} - \frac{5}{2} = \frac{1}{2} v_2^2 \)
\( \frac{4}{2} = \frac{1}{2} v_2^2 \)
\( 2 = \frac{1}{2} v_2^2 \)

12. Multiply both sides by 2:
\( 4 = v_2^2 \)

13. Take the square root:
\( v_2 = \sqrt{4} = 2 \, \text{m/s} \)

Final Answer:
The speed of the pendulum bob when it makes an angle of \( 60^\circ \) with the vertical is \( 2 \, \text{m/s} \).