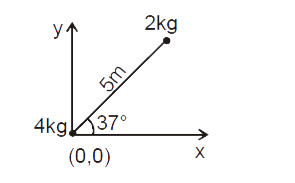
A body of mass 2.5 kg is subjected otthe forces shown in figure. Find the aceleration o thecentre of maas.
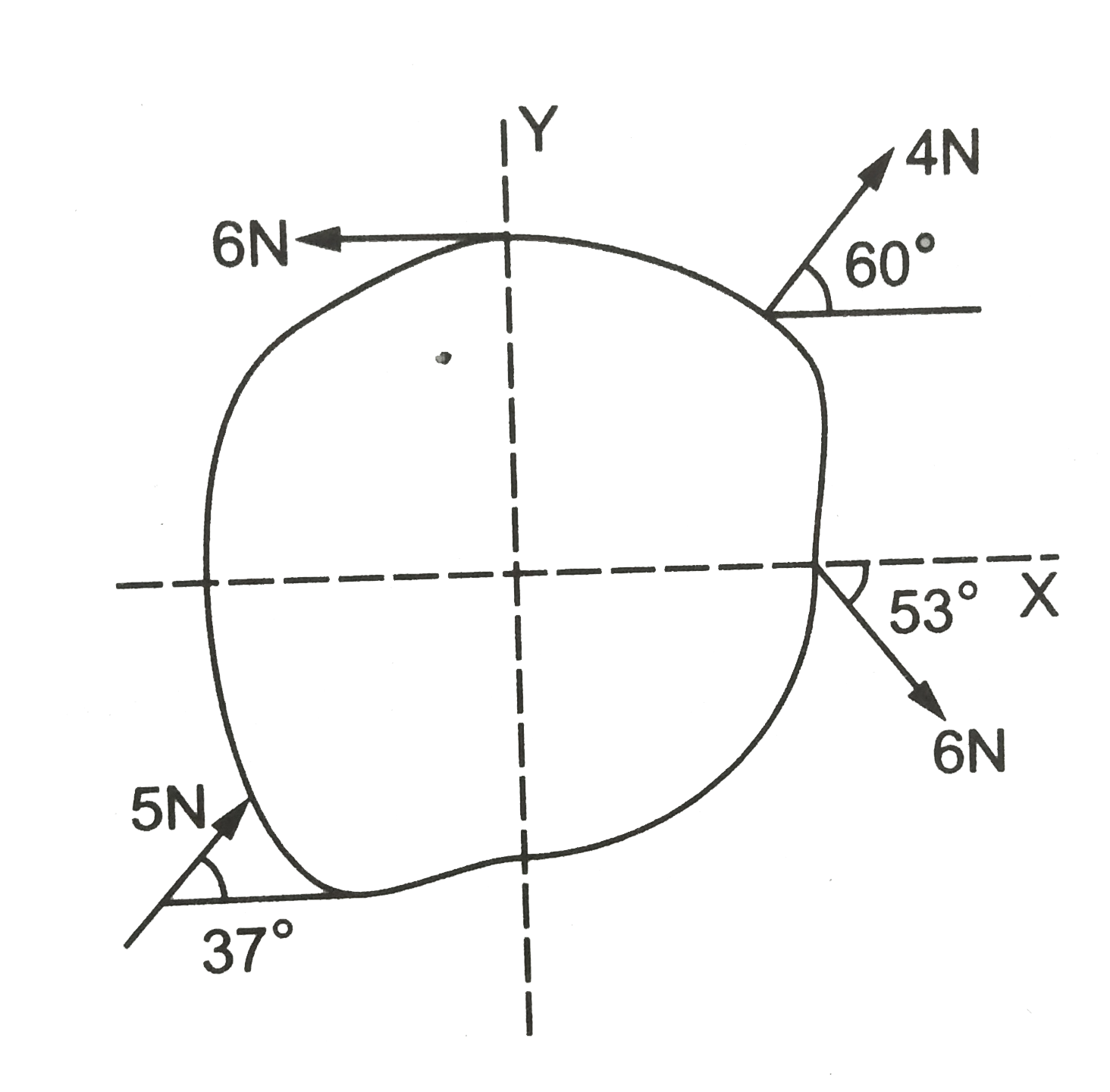
Take the X andy axes as shown in theure. The x-component of the resultant force is
Fx=−6N+(5N)cos370+(6N)cos530+(4N)cos600
=−6N+(5N).(45)+(6N).(35)+(4N).(12)=3.6N
similarly the y component of the resultant force is
Fy=5Nsin370−(6N)sin530+4Nsin600
=(5N).(35)−(6N).(45)+(4N).(√32)=1.7N
The magnitude of the resultant force is
F=√F2x+F2y=√(3.6N)+(1.7N)2≈4.0N
The direction of the resultant force makes an angle θ
with the X-axis where
tantheta=F_y/F_x=1.7/3.6=0.47<br>The acceleration of the centre of mass is
aCM=FM=4.0N2.5kg=1.6ms2
in the direction of the resultant force

Similar Questions
Knowledge Check
A body of mass 2kg is kept on a rough horizontal surface as shown in the figure. Find the work done by frictional force in the interval t=0 to t=5sec
 AzeroB+15JC−20JDdata insufficient
AzeroB+15JC−20JDdata insufficientA body of mass 5kg initially at rest, is subjected to a force of 40 N. Find the kinetic energy acquired by the body at the end of 5 seconds :
A4000 JB6000 JC6249 JD6145 NFor body of 50 kg. mass, the velocity time graph is shown in figure. Then force acting on the body is :-
 A25NB50NC12.5 ND100 N
A25NB50NC12.5 ND100 N
Three block of masses 1kg,4kg and 2kg are placed on a smooth horizontal plane as shown in figure. Find
(a) the acceleration of the system,
(b) the normal force between 1kg block and 4kg block,
( c) the net force on 2kg block

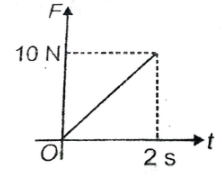
View SolutionA variable force acts on a body of mass 2 kg initially at rest as shown in figure . Calculate the impulse of the force in first 2 seconds and speed of the body after 2 seconds .
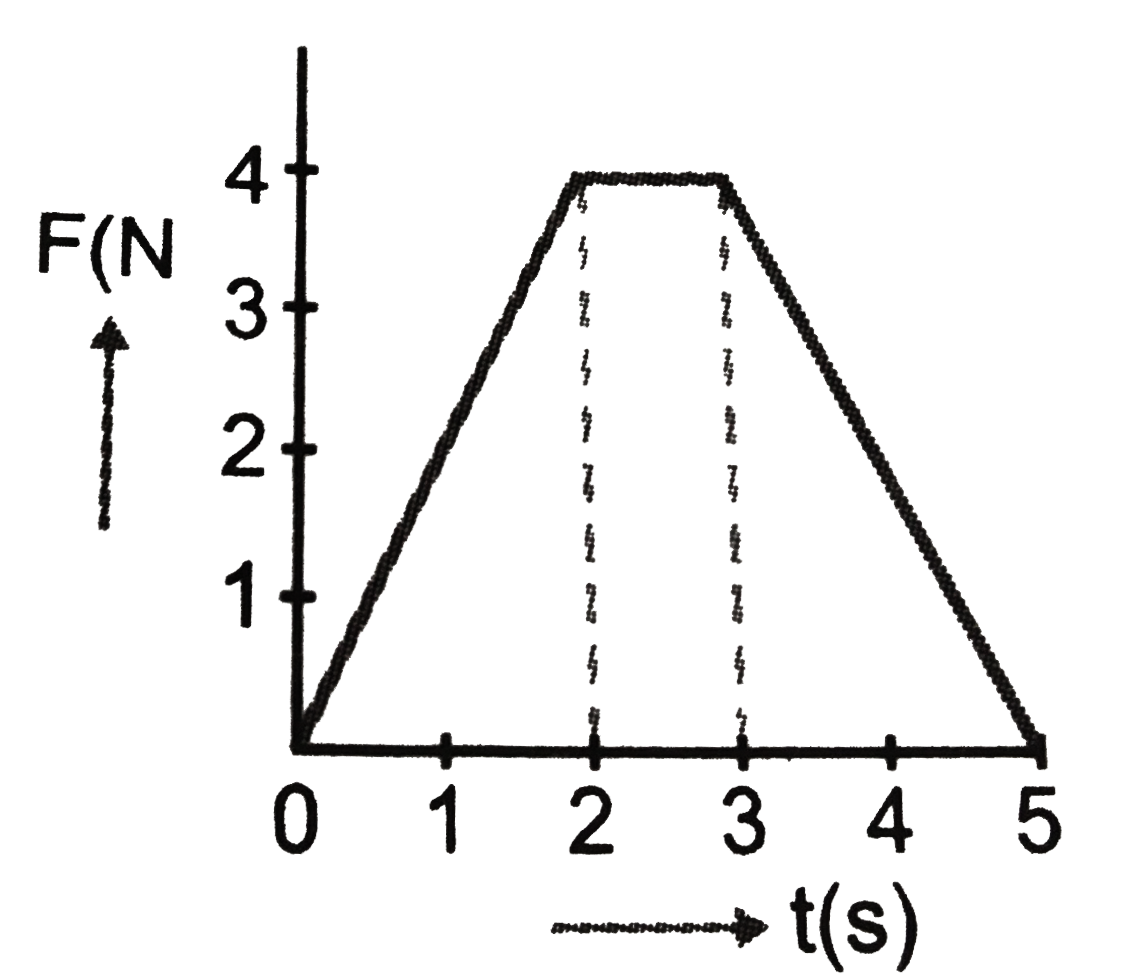
View SolutionA force acting on a body of mass 2 kg varies with time as shown in fig . 20 find impulse of the force and final velocity of the body.
View SolutionA force of 50 N acts in the direction as shown in figure. The block of mass 5kg. Resting on a smooth horizonatal surface. Find out the acceleration of the block.
View SolutionA force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
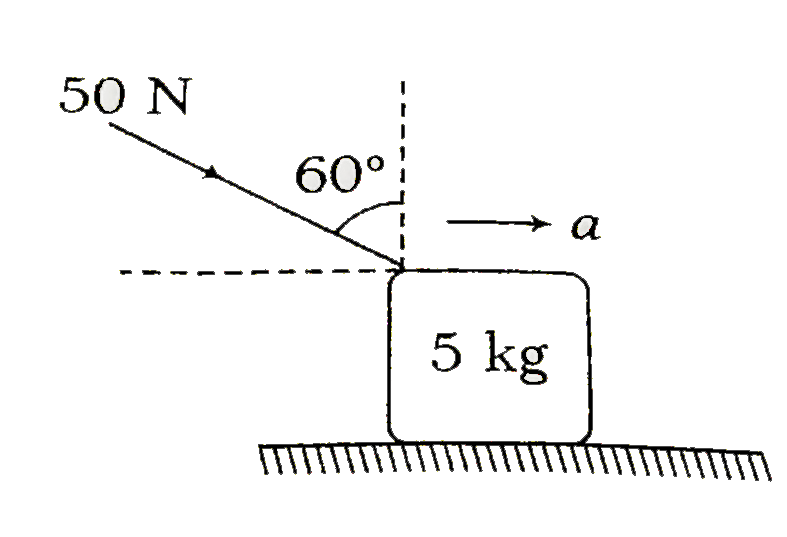
View Solution