Light in certain cases may be considered as a stream of paerticles called photons. Each photon has a linear momentum hλ where h is the Planck's constant and λ is the wavelength λ is incident on a plane mirror at an angle of incidene θ. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
P(ncnce)(hλ)cosθ→i−(hλ0sinθ→j
PRef≤cted=−(hλ)cosθ→i−(hλ)sinθ→j
The change in momentum will be only in the x-axis direction i.e.
|△P|=(hλcosθ−(hλcosθ)<br>=((2h)/lamda) costheta
Topper's Solved these Questions
Similar Questions
A photon has an energy
where h is the Planck's constant, v is the frequency of radiation, λ is the wavelength of radiation, and c is the velocity of light.View SolutionIf energy of photon is E∝hacbλd.
Here h= Planck's constant c= speed of light and
λ= wavelength of photon
Then, the value of a,b and d areView Solution
Knowledge Check
- Question 1 - Select One
When a hydrogen atoms emits a photon of energy 12.1eV , its orbital angular momentum changes by (where h os Planck's constant)
A3hπB2hπChπD4hπ - Question 2 - Select One
If the enrgy of a frequency v is gives by E=hv where h is plank's constant and the momentum of photon is p=h/λ where λ is the wavelength of photon , then the velocity of light is equal to
A(Ep)12BEpCEpD(Ep)2 - Question 3 - Select One
We may state that the energy E of a photon of frequency v is E =hv, where h is a plank's constant. The momentum p of a photon is p=h/λ where λ is the wavelength of the photon. From the above statement one may conclude that the wave velocity of light is equal to
A3×108m/sBE/pCEpD(E/p)2
According to Planck's quantum theory of light, every source of radiation emits photons (i.e., packets of energy ) which travel in all directions with the same speed (i.e., speed of light). Each photon is of energy E=hv=hc/λ, where h is Planck's constant, v is the frequency and λ is wavelength of radiation emitted. The photons emitted from different sources of radiation are different. Read the above passage and answer the following questions:
(i) on what factors does the number of photons emitted per second from a source of radiations depends?
(ii) Why are the high energy photons not vissible to eye?
(iii) Which basic values do you learn from this study?View SolutionA parallel beam of monochromatic light of wavelength 663 nm is incident on a totally reflection plane mirror. The angle of incidence is 60∘ and the number of photons striking the mirror per second is 1.0×1019. Calculate the force exerted by the light beam on the mirror.
View SolutionA parallel beam of monochromatic light of wavelength 663 nm is incident on a totally reflecting plane mirror. The angle of incidence is 60∘ and the number of photons striking the mirror per second is (1.0×(1019)). Calculate the force exerted by the light beam on the mirror.
View Solution_E01_104_Q01.png)
Two plane mirrors, a source S of light, wmitting monochromatic rays of wavelength λ and a screen are arranged as shown in figure. If angle θ is very small, calculate fringe width of the interference pattern formed by reflected rays.View SolutionIn the photoelectric effect the eletrons are emiited intantaneously from a given matal plate when it is irradiated with radiation of frequency equal to or greater then some minimum ferquency, is called the threshold frequency.According to Planck's idea, light may be considered to be made up discrete particles called photons.Each photon carries energy equal ti hv.When this photon cllides with the electron of the metal, the electron acquires energy of the emitted electron is given by :
hv=K.Emaximum+PE=12mu2+PE
If the incident rediation is of threshold frequency the electron will be emitted without any kinetic energy
i.e hv0
∴12mu2=hv−hv0
A plot of kinetic energy of the emitted electron versus frequency of the incident radiation yields a straight line given as :
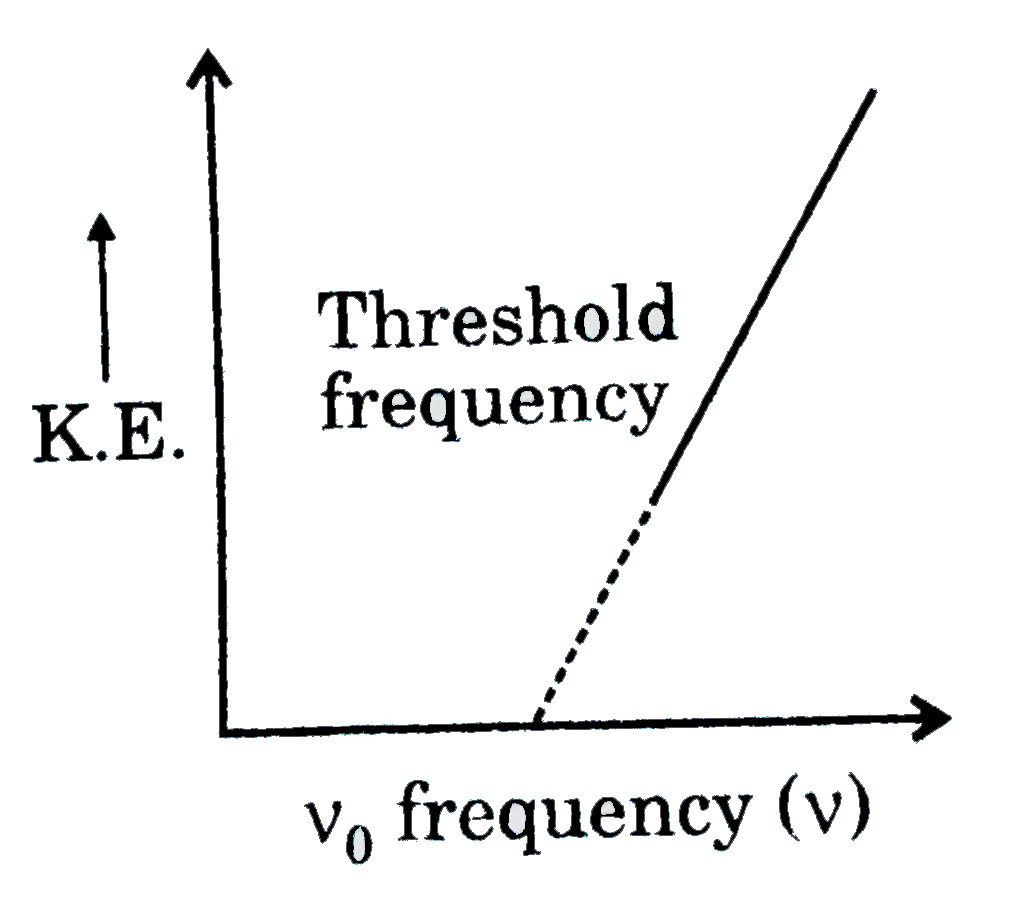
A beam of white light is dispersed into its wavelenght components of potassium metal. What of the electron emitted by the different light component ?View Solution