Suppose the friction coefficient between the ground and the ladder of the previous problem is 0.540. Find the maximum weight of a mechanic who could go up and do the work from the same position of the ladder.
The correct Answer is:D
μ=0.54,R2=16g+mg,R1=μR2
→R1×10cos37∘=16g×5xsin37∘+mg×8sin3∘
→8R1=48g+245mg
→R2=48g+245mg8×0.54
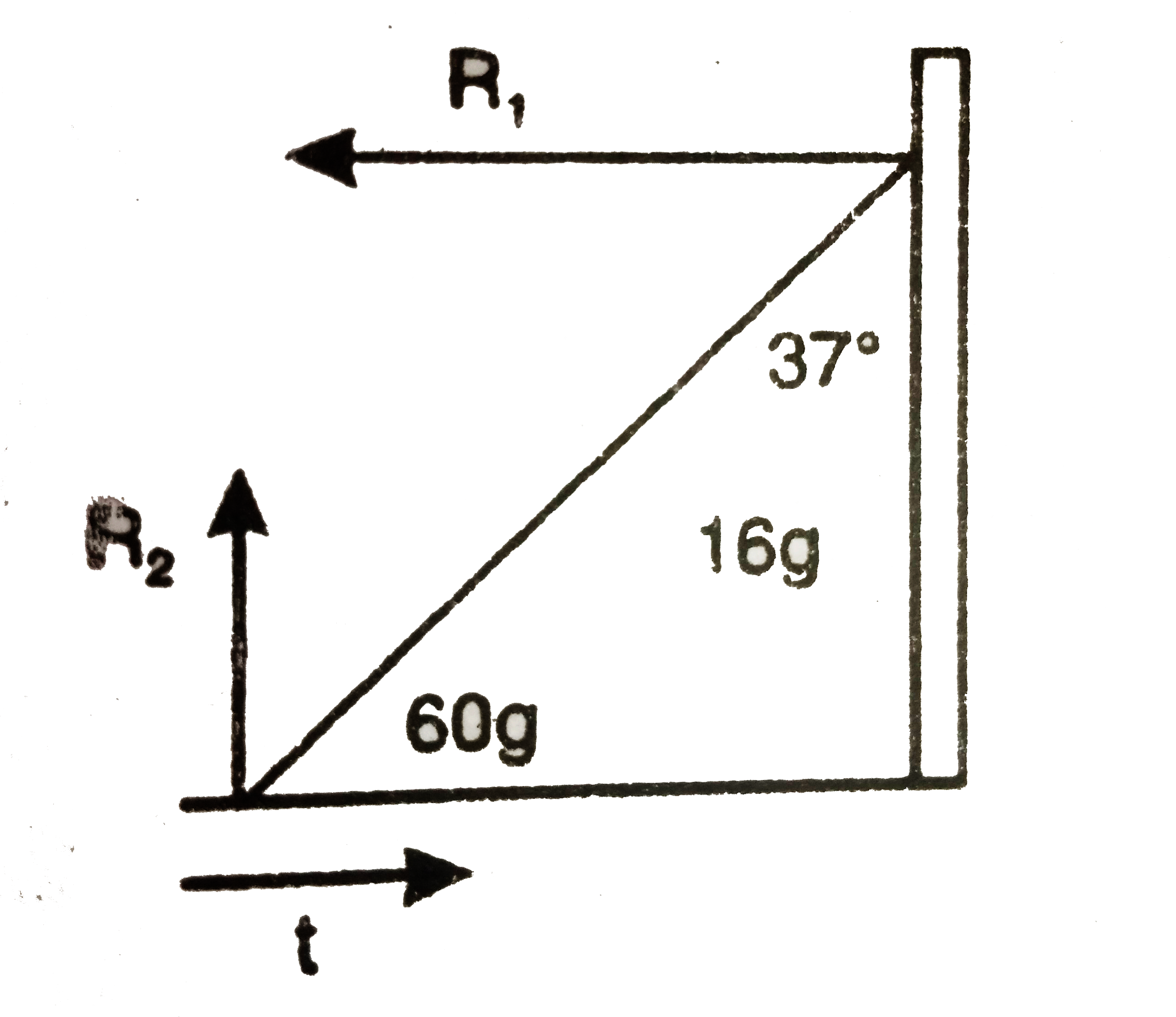
→16g+mg=240g+24mg5x8x0.54
→16+m=240+24m40×0.54
→m=44kg
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
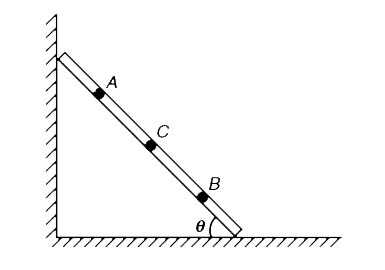
A ladder of mass M and length L stays at rest against a smooth wall. The coefficient of friction between the ground and the ladder is μ
(a) Let Fwall, W and Fg be the force applied by wall, weight of the ladder and force applied by ground on the ladder. Argue to show that the line of action of these three forces must intersect.
(b) Using the result obtained in (a) show that line of action of Fg makes an angle tan−1(2tanθ) with the horizontal ground where θ is the angle made by the ladder with the ground.
(c) Find the smallest angle that the ladder can make with the ground and not slip.
(d) You climb up the ladder, your presence makes the ladder more likely to slip. Where are you at A or B? C is the centre of mass of the ladder.
View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View Solution
Knowledge Check
A uniform ladder 5.0m long rests against a frictionless, vertical wall with its lower end 3.0m to from the wall. The ladder weighs 160N. The coefficient of static friction between the foot of the ladder and the ground is 0.40. A man weighing 740N climbs slowly up the ladder.
How far along the ladder can the man climb before the ladder starts to slip?A3mB5mC2.7mD1.25mA uniform ladder 5.0m long rests against a frictionless, vertical wall with its lower end 3.0m to from the wall. The ladder weighs 160N. The coefficient of static friction between the foot of the ladder and the ground is 0.40. A man weighing 740N climbs slowly up the ladder.
What is the maximum frictional force that the ground can exert on the ladder at its lower end?A360NB171NC900ND740NA uniform ladder 5.0m long rests against a frictionless, vertical wall with its lower end 3.0m to from the wall. The ladder weighs 160N. The coefficient of static friction between the foot of the ladder and the ground is 0.40. A man weighing 740N climbs slowly up the ladder.
What is the actual frictional force when the man has climbed 1.0m along the ladder?A360NB171NC900ND740N
A 6.5 m long ladder rests against as vertical wall reaching a height of 6.0 m. A 60 kg man stands hlf way up the ladder. A. Find the torque of the force exerted by the man on the ladder bout the upper end of the ladder. b.Assuming the weight of the ladder of be negligible as compared to the man and assuming the wall to be smooth find the force exerted by the ground on the ladder.
View SolutionA block of mass 10 kg slides down on an incline 5 m long and 3 m high. A man pushes up on the ice block parallel to the incline so that it slides down at constant speed. The coefficient of friction between the ice and the incline is 0.1. Find :
(a) the work done by the man on the block.
(b) the work done by gravity on the block.
(c) the work done by the surface on the block.
(d) the work done by the resultant forces on the block.
(e) the change in K.E. of the block.
View SolutionThe friction coefficient between the two blocks shown in figure is μ and the horizontal plane is smoth. (a) if the systeam is slightly displacement and released, find the time period. (b) Find the magnitude of the fricational force between the blocks when the displacement from the fmean position is x. (c) What can be the maximum amplitude if the upper block does not slip relative to the lower block ?
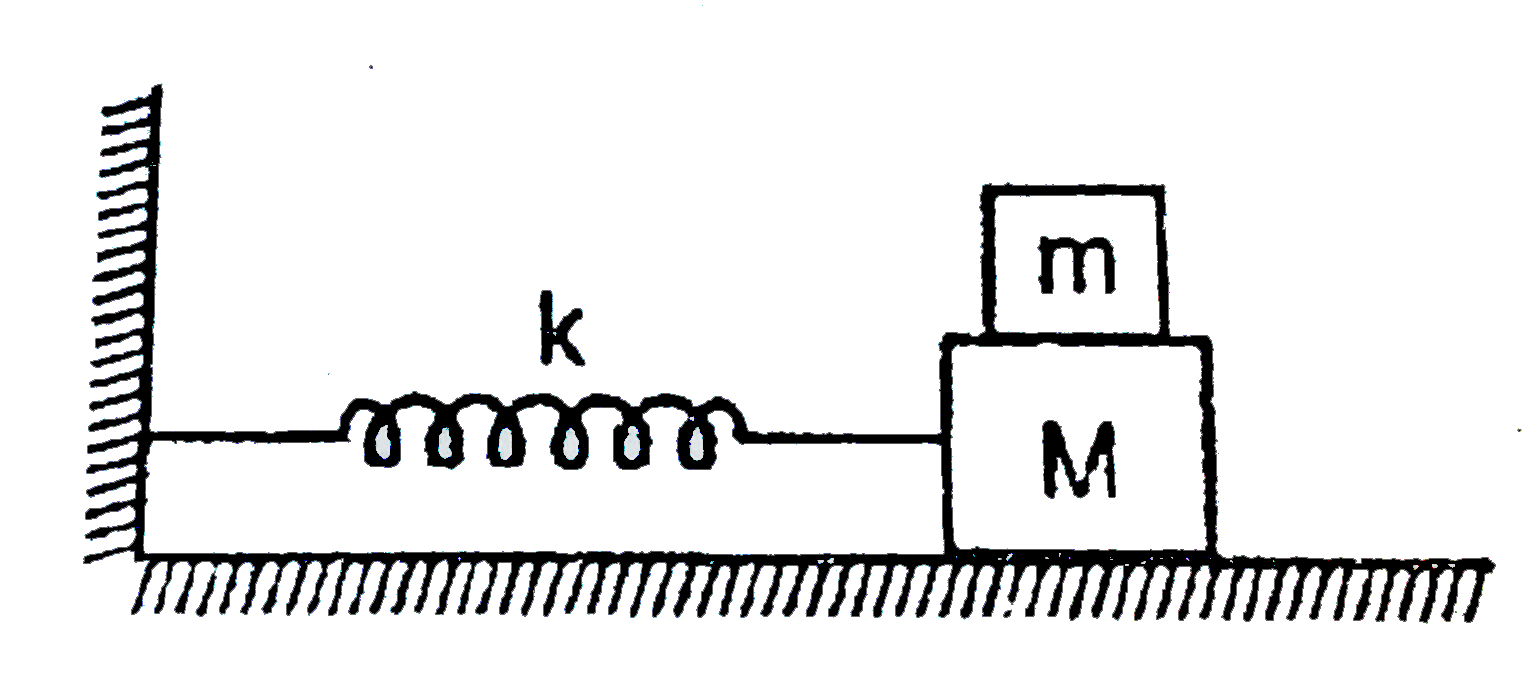
View SolutionA car is taking a turn of radius 400 m on a horizontal circle . Coefficient of friction between the ground and tyres of car is 0.2 . Find the maximum speed with a safe turn can be taken
View SolutionA block mass m=2kg is moving with velocityv0 towards a massless unstretched spring of the force constant k=10N/m. Coefficient of friction between the block and the ground is μ=0.2. Find the maximum value of v0 so that after pressing the spring the block does not return back but stops there permanently.

View Solution
