Pressure of 1 mole ideal is given by
P=P0[1−12(V0V)2] V0 to 2V0. Find change in temperature.
5P0V04R
P0V4R
3P0V4R
P0V2R
The correct Answer is:A
Step by step video, text & image solution for Pressure of 1 mole ideal is given by P=P_(0)[1-(1)/(2)(V_(0)/(V))^(2)] ,brgt If volume of gas change from V_(0) to 2 V_(0). Find change in temperature. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
One mole. of an ideal gas undergoes a process P=P01+(V0V)2. Here P0 and V0 are constants. The change in temperature of the gas when volume is changed from V=V0 to V=2V0 is xP0V010R. Find x. (Here R= Universal gas constant)
View SolutionOne mole of an ideal gas undergoes a process
p=p01+(VV0)2
where p0and V0 are constants. Find temperature of the gaas when V=V0.
View Solution
Knowledge Check
Pressure of an ideal gas is given by
P=P0=[1−12(V0V)2]AP0V03RB5P0V04RC4P0V0RD3P0V0ROne mole of an ideal gas undergoes a process P=P0[1+(2V0V)2]−1, where P0V0 are constants. Change in temperature of the gas when volume is changed from V=V0→V=2V0 is:
A45P0V0nRB34P0V0nRC23P0V0nRD97P0V0nROne mole of an ideal gas undergoes a process p=p01+(V0V)2. Here, p0 and V0 are constants. Change in temperature of the gas when volume is changed from V=V0 to V=2V0 is
A−2p0V05RB11p0V010RC−5p0V04RDp0V0
In process T∝1V, pressure of the gas increases from p0 to 4p0. Match the following.
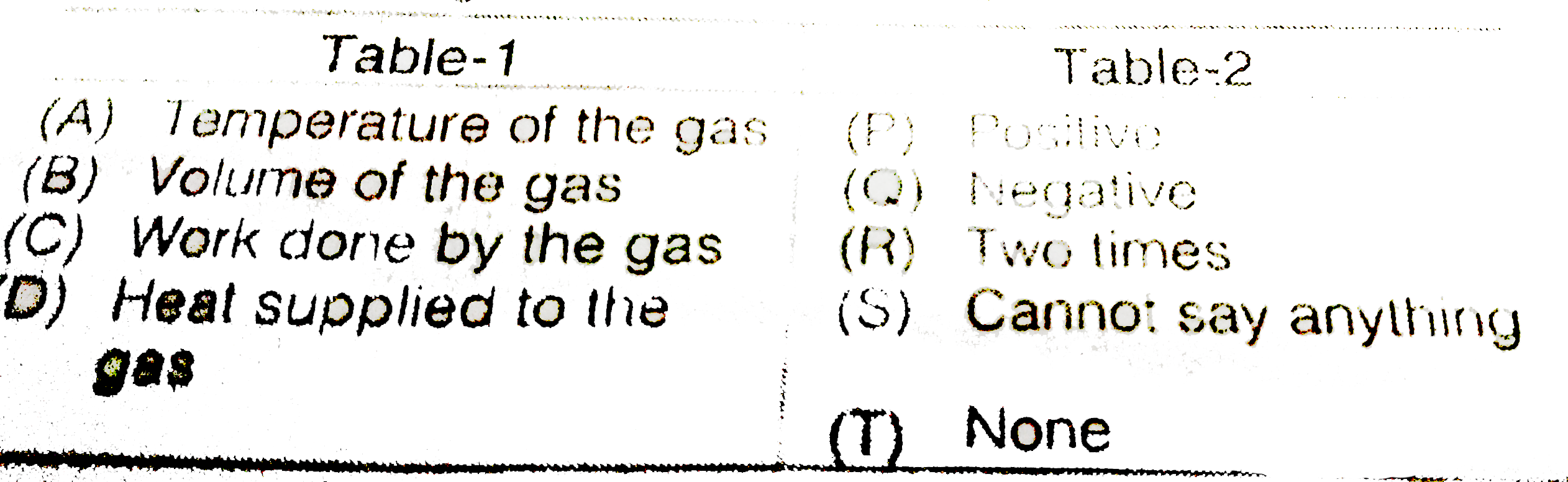
View SolutionFor one mole of ideal gas if P=P01+(VV0) where P0 and V0 are constant, then temperature of gas when V=V0 is:
View SolutionOne mole of an ideal gas passes through a process where pressure and volume obey the relation P=P0[1−12(V0V)2] Here P0 and V0 are constants. Calculate the change in the temperature of the gas if its volume changes from V0 to 2V0.
View SolutionOne mole of ideal gas goes through processP=2V21+V2. Then change in temperature of gas when volume changes from V=1m2 to 2m2 is :
View SolutionThe work done in changing the state from (P0,V0) to (P1,V1) in the following system is :
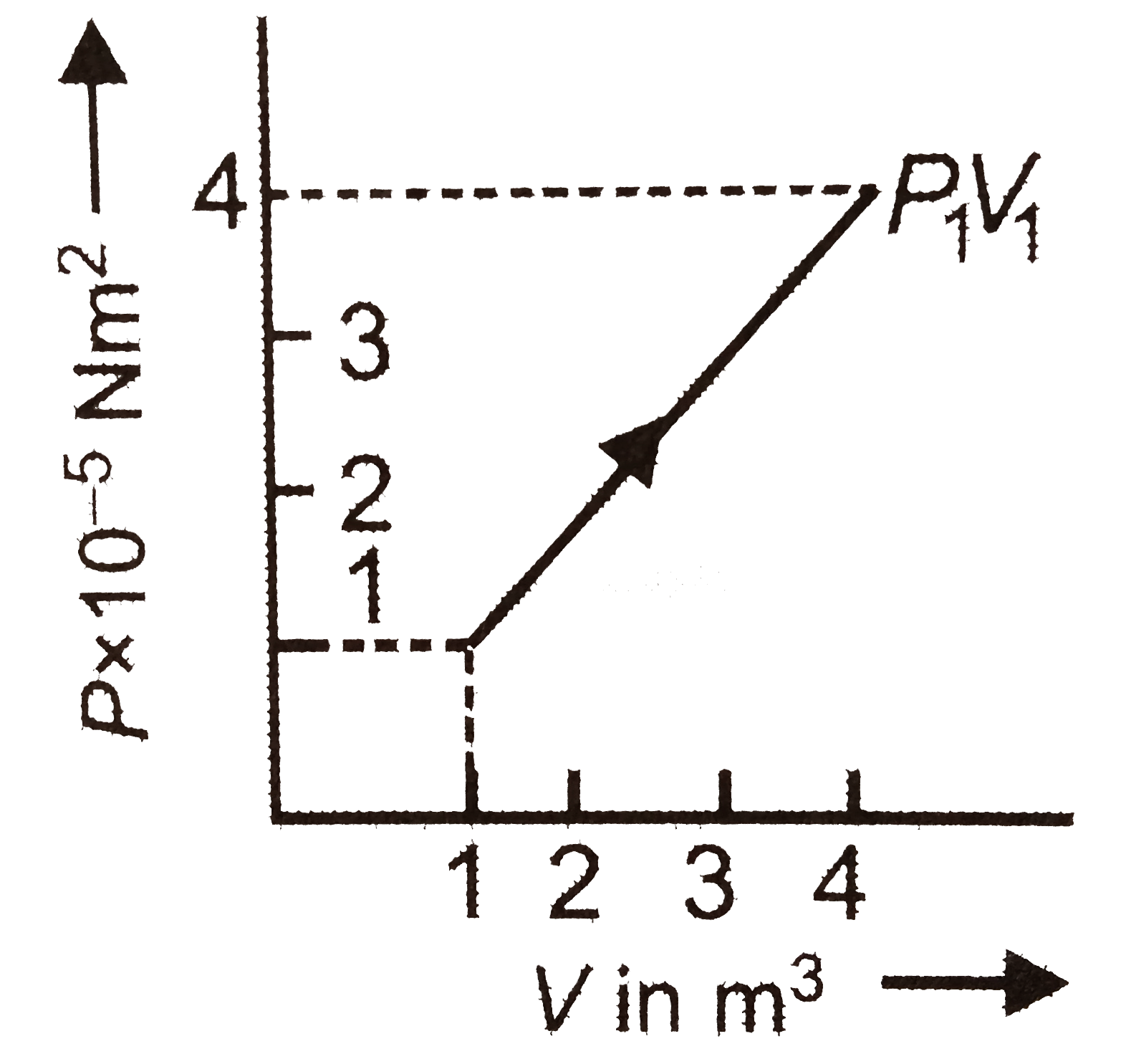
View Solution
