Derive an expression fro the gravitational field due to a unifrom rod of length L and M at a point on its perpendicular bisector at a distance d from the centre.
The correct Answer is:B, D
To derive the expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the center, we can follow these steps:
Step 1: Define the system
Consider a uniform rod of length L and mass M. We want to find the gravitational field at point P, which is located on the perpendicular bisector of the rod at a distance d from the center of the rod.
Step 2: Divide the rod into small elements
We can divide the rod into infinitesimally small elements of length dx. The mass of each small element dm can be expressed as:
dm=MLdx
where ML is the mass per unit length of the rod.
Step 3: Determine the distance from the element to point P
Let x be the distance from the center of the rod to the small element dx. The distance r from the element dm to point P is given by:
r=√d2+x2
Step 4: Calculate the gravitational force due to the element
The gravitational force dF exerted by the small mass dm on a test mass m placed at point P is given by Newton's law of gravitation:
dF=GMdmr2=GM(MLdx)d2+x2
Step 5: Resolve the gravitational force into components
The gravitational force dF can be resolved into two components: one along the vertical direction (towards the rod) and one along the horizontal direction. The vertical component dFy is given by:
dFy=dFcosθ
where cosθ=d√d2+x2. Thus,
dFy=GM(MLdx)d2+x2⋅d√d2+x2=GM2dL(d2+x2)3/2dx
Step 6: Integrate to find the total gravitational force
To find the total gravitational force Fy acting on the mass m at point P, we need to integrate dFy from −L2 to L2:
Fy=∫L2−L2GM2dL(d2+x2)3/2dx
Step 7: Evaluate the integral
The integral can be evaluated using the substitution x=dtanθ:
dx=dsec2θdθ
Changing the limits accordingly, we can solve the integral:
Fy=GM2dL∫tan−1(L/2d)−tan−1(L/2d)sec2θ⋅1(d2(1+tan2θ))3/2dθ
Step 8: Final expression for gravitational field
After evaluating the integral, we find the total gravitational field E at point P by dividing the total gravitational force Fy by the mass m:
E=Fym=2GMd√L2+4d2
Final Result
Thus, the expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the center is:
E=2GMd√L2+4d2
Consider a uniform rod of length L and mass M. We want to find the gravitational field at point P, which is located on the perpendicular bisector of the rod at a distance d from the center of the rod.
We can divide the rod into infinitesimally small elements of length dx. The mass of each small element dm can be expressed as:
dm=MLdx
where ML is the mass per unit length of the rod.
Let x be the distance from the center of the rod to the small element dx. The distance r from the element dm to point P is given by:
r=√d2+x2
The gravitational force dF exerted by the small mass dm on a test mass m placed at point P is given by Newton's law of gravitation:
dF=GMdmr2=GM(MLdx)d2+x2
The gravitational force dF can be resolved into two components: one along the vertical direction (towards the rod) and one along the horizontal direction. The vertical component dFy is given by:
dFy=dFcosθ
where cosθ=d√d2+x2. Thus,
dFy=GM(MLdx)d2+x2⋅d√d2+x2=GM2dL(d2+x2)3/2dx
To find the total gravitational force Fy acting on the mass m at point P, we need to integrate dFy from −L2 to L2:
Fy=∫L2−L2GM2dL(d2+x2)3/2dx
The integral can be evaluated using the substitution x=dtanθ:
dx=dsec2θdθ
Changing the limits accordingly, we can solve the integral:
Fy=GM2dL∫tan−1(L/2d)−tan−1(L/2d)sec2θ⋅1(d2(1+tan2θ))3/2dθ
After evaluating the integral, we find the total gravitational field E at point P by dividing the total gravitational force Fy by the mass m:
E=Fym=2GMd√L2+4d2
Thus, the expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the center is:
E=2GMd√L2+4d2
Topper's Solved these Questions
Similar Questions
The radius of gyration of a uniform rod of mass m and length l about an axis perpendicular to its length and at distance l4 from its one end will be
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View Solution
Knowledge Check
The magnetic field due to current in a straight wire segment of length L at a point on its perpendicular bisector at a distance r(r>>L)
Adecreases as 1rBdecreases as tr2Cdecreases as 1r3Dapproaches a finite limit as r→∞The moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
AML26BML212C7ML224D7ML248If Ea be the electric field strength of a short dipole at a point on its axial line and Ee that on the equatorial line at the same distance, then
AEa=ErBEa=2ErCEr=2EaDEa=√2Er
Calculate the field due to a uniformly charged straight conductor of length 2j at a distance d along its perpendicular bisector. The charge on the conductor is q.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionA uniform rod of mass m and length l is taken. Find the gravitational field intensity at point P at distance d which is on the perpendicular bisector of the rod as shown in Fig.
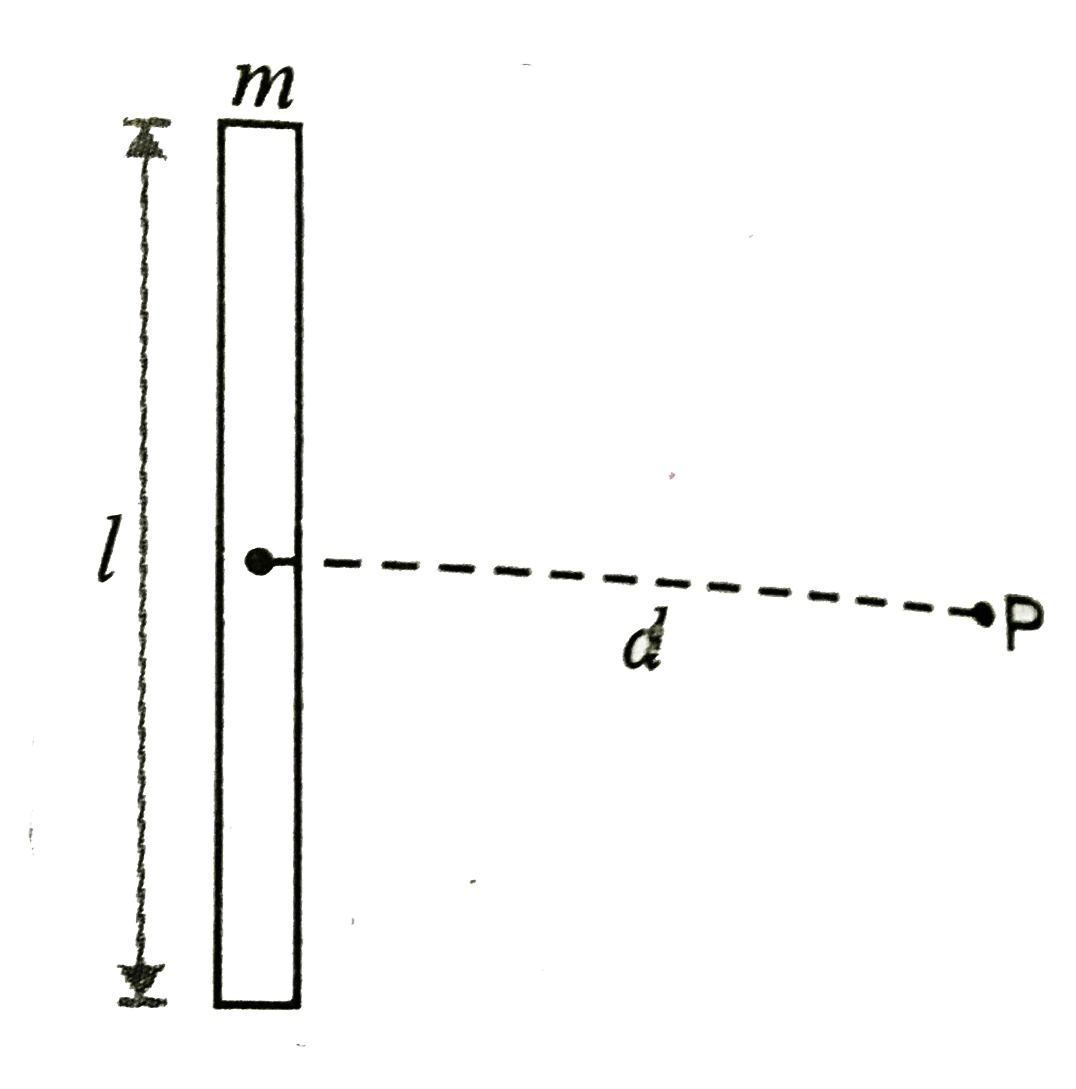
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionThe radius of gyration of rod of length L and mass M about an axis perpendicular to its length and passing through a point at a distance L/3 from one of its ends is
View Solution
