A simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π3 seconds to complete one oscilation. Find the acceleration of the elevator.
The correct Answer is:4ftsec2
Let the elevator be moving upward acceleration a0
Here driving force
f=m(g−a0)sinθ
Acceleration =(g+a0)θ=(g−a0)θ(sinθ→θ)
=(g+a0)xl=ω2x
T=2π√lg+a0
Given that T=π3sec,l=1ft
and g=32ftsec2
=π3=2π√132+a0
19=4(132+a)
→32+a=36
a=36−32=4ftsec2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A simple pendulum of length l is suspended throught the ceiling of an elevator. Find the time period of small oscilations if the elevator a. is going up with an acceleration a0. b. is going down with an acceleration a0 and c. is moving with a uniform velocity.
View SolutionA pendulum of mass m and length l is suspended from the ceiling of a trolley which has a constant acceleration a in the maximum deflection θ of the pendulum from the vertical.
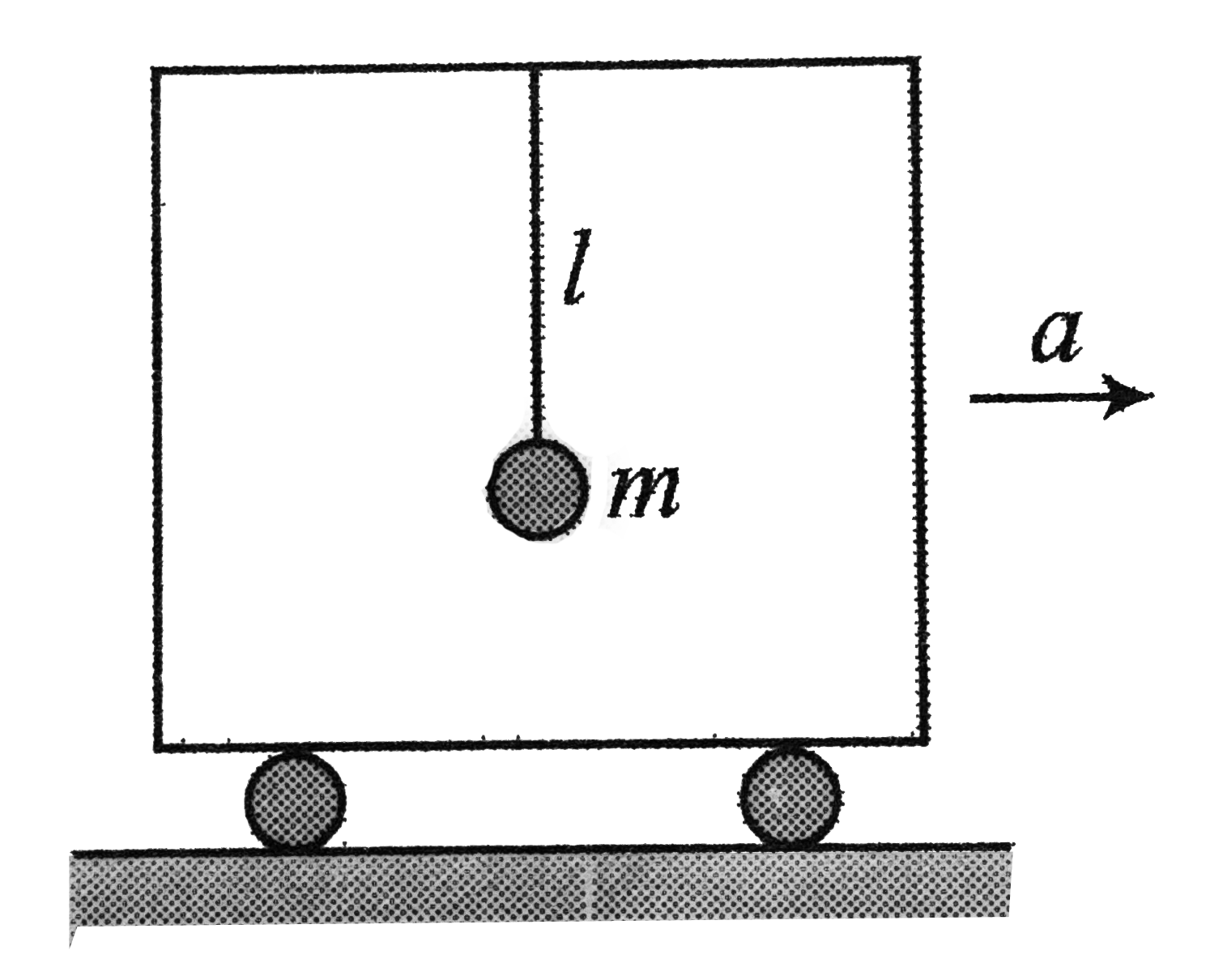
View Solution
Knowledge Check
A simple pendulum of length 1 m is freely suspended from the ceiling of an elevator. The time period of small oscillations as the elevator moves up with an acceleration of 2m/s2 is (use g=10m/s2)
Aπ√5 sB√25πsCπ√2 sDπ√3 sA simple pendulum completes 10 oscillation in 30 second. Another simple pendulum takes 40 seconds to complete 10 oscillations at the same place. The ratio of the lengths of the simple pendulums is
A516B916C316D1316A simple pendulum of length 5 m is suspended from the ceiling of a cart. Cart is sliding down on a frictionless surface having angle of inclination 60°. The time period of the pendulum is
A2πsBπsC4πsDπ2s
A pendulum suspended from the ceiling of an elevator at rest has a time period of oscillation equal to T1. When the elevator moves up with an acceleration a, the time period becomes T2 and when the elevator moves down with an acceleration a, its time period becomes T3, then find the expression for T1 in terms of T2 and T3.
View SolutionA train is travelling at a constant speed u around a circular track of radius R. A simple pendulum of length L and mass m is suspended from the ceiling of the compartment of the train. IF the tension in the string of the pendulum is T, then find the time period of oscillation.
View SolutionAa simple pendulum is suspended from the ceiling of a vehicle which moves down an inclined plane o inclination Θ. The period of oscilation of the pendulum is
View SolutionA simple pendulum of length L is suspended from the roof of a train. If the train moves in a horizontal direction with an acceleration 'a' then the period of the simple pendulum is given by
View SolutionA simple pendulum takes 32 s to complete 20 oscillations. What is the time period of the pendulum?
View Solution
