A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass135∘ and surface tension of mercury =0.465Nm−1. Density of mercury=13600kgm−3.
The correct Answer is:C
r=1.0mm,<br>p=76cm,
θ=135∘,T=0.4654Nm
h=2Tcosθrρg
θ=135∘,t=0.465Nm
h=2×465×(1√2)10−3×13600×10=0.0048m
=0.48cm
=capillary fault due to surface tension
So, height raised in barometer tube
=H−h=76−0.48=75.52cm
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective 2
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
Similar Questions
What will be the length of mercury column in a barometer tube when the atmosperic pressure is 75cm of mercury and the tube is inclined at an angle of 60∘ with the horizontal direction?
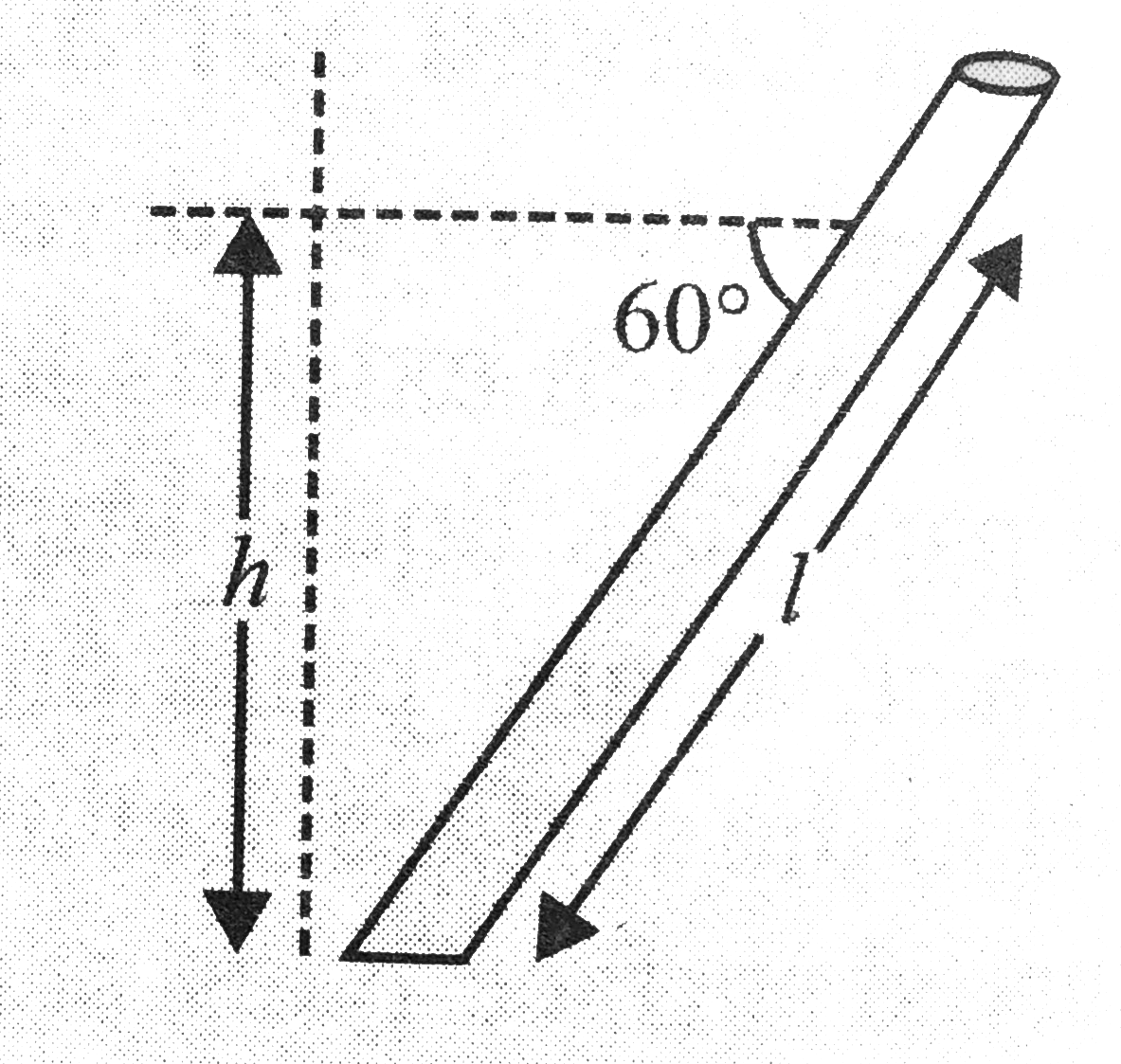
View SolutionA satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1m long placed inn the satellite?
View Solution
Knowledge Check
Suppose the pressure at the surface of mercury in as barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
AP1=0,P2= atgmospheric pressureBP1= atmosphereic pressure P2=0CP1=P2=atmospheric pressureDP1=P2=0What will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle ϕ with the vertical direction ?
AxsinϕBxcosϕCxtanϕDxThe excess pressure inside mercury drop of diameter 4 mm is (Take surface tension of mercury is 0.465 N/m)
A410 PaB465 PaC610 PaD310 Pa
What will be the length of mercury column in a barometer tube, when the atmospheric pressure is 76 cm of mercury and the tube is inclined at an angle of 30∘ with the horizontal direction ?
View SolutionFind the excess pressure inside a mercury drop of radius 2.0 mm. The surface tension oif mercury 0.464Nm−1.
View SolutionA faulty barometer tube is 90cm long and its contains some air above mercury. The reading is cm when the true atmospheric pressure 76cm. What will be the true atmospheric pressure if the reading on this barometer is 74 cm? (H = 10cm of water column)
View SolutionCalculate the equivalent height of water barometer if the pressure recorded by mercury barometer is 76 cm. Density of mercury is 13600kgm−3 and density of water is 1000kgm−3.
View SolutionIf the mercury in the barometer is replaced by water, what will be the resulting height of the water column? Density of water =1000kgm−3 density of mercury =13600kgm−3
View Solution
