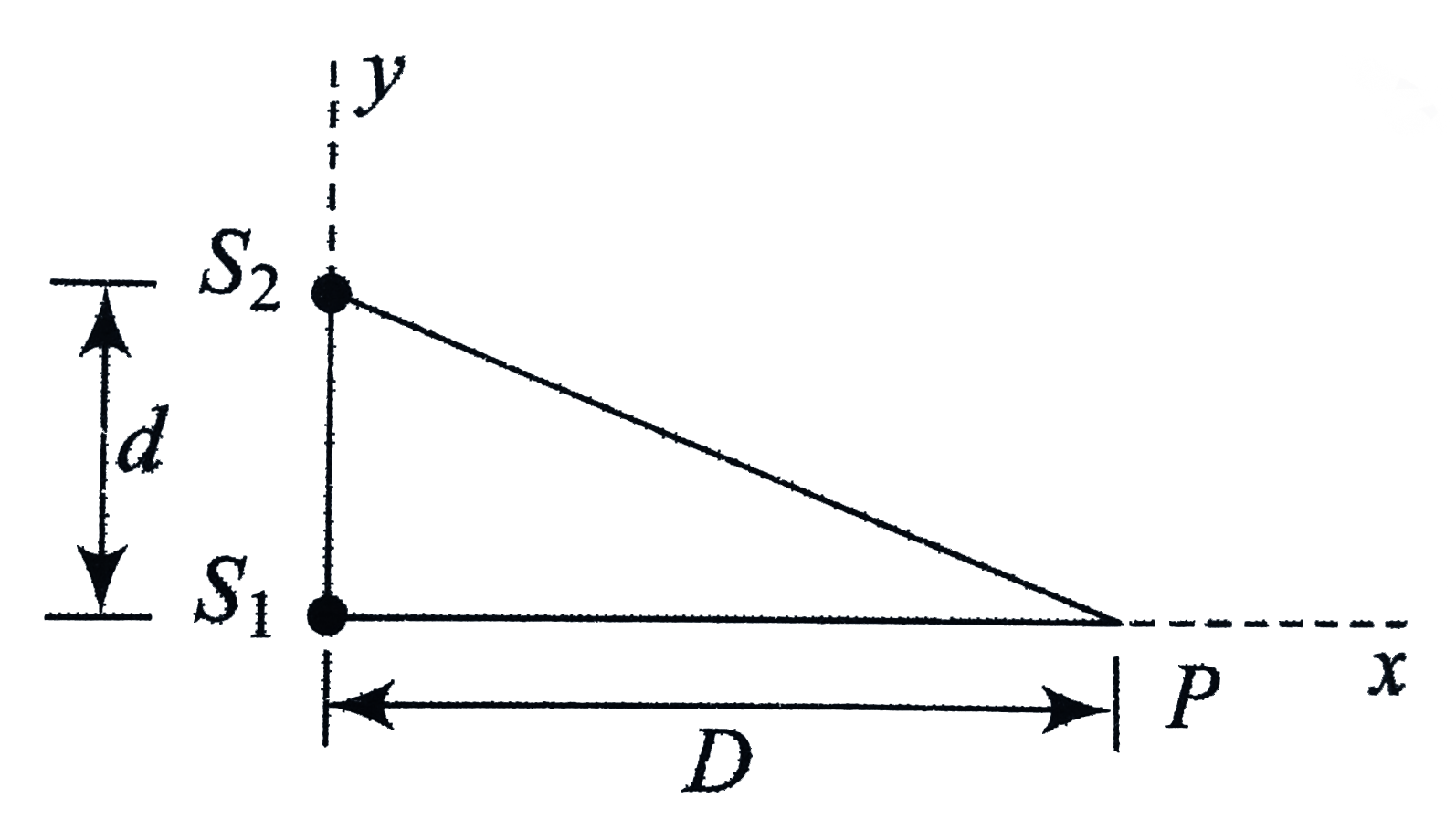
Two sources S1andS2 emitting light of wave length 600 nm are placed a distance 1.0x10−2 cm apart. A detector can be moved on the litre line S1P which is perpendicular to S1S2. a.What would be the minimum and maximum path differrence at the detector as it is moved alog the line S1P? b. Locate the position of the farthest minimum detect.
To solve the problem step by step, we will break it down into parts (a) and (b) as given in the question.
Part (a): Minimum and Maximum Path Difference
1. Understanding the Setup:
- We have two sources, S1 and S2, separated by a distance d=1.0×10−2 cm.
- The wavelength of the light emitted by these sources is λ=600 nm (which is 600×10−9 m).
- A detector moves along the line S1P, which is perpendicular to the line S1S2.
2. Finding Minimum Path Difference:
- The minimum path difference occurs when the detector is positioned such that the light from both sources reaches it at the same time.
- This happens when the detector is very far away from the sources, ideally at infinity, or when it is directly in line with S1.
- Therefore, the minimum path difference is Δxmin=0.
3. Finding Maximum Path Difference:
- The maximum path difference occurs when the detector is positioned such that the distance from S2 to the detector is maximized.
- This happens when the detector is directly in line with S2 (i.e., at point S2).
- The path difference in this case is equal to the distance between the two sources, which is Δxmax=d.
4. Calculating the Values:
- Convert d from cm to meters:
d=1.0×10−2 cm=1.0×10−4 m
- Thus, the maximum path difference is:
Δxmax=1.0×10−4 m
Summary for Part (a):
- Minimum Path Difference: Δxmin=0
- Maximum Path Difference: Δxmax=1.0×10−4 m
---
Part (b): Locating the Position of the Farthest Minimum Detector
1. Understanding Conditions for Minima:
- For destructive interference (minima), the path difference must be an odd multiple of half the wavelength:
Δx=(m+12)λ(m=0,1,2,…)
2. Using the Geometry:
- Let D be the distance from S1 to the detector along the line S1P.
- The path lengths from S1 and S2 to the detector can be calculated using the Pythagorean theorem:
S1P=D,S2P=√D2+d2
- The path difference is given by:
Δx=S2P−S1P=√D2+d2−D
3. Setting Up the Equation for Minima:
- For the first minimum (m=0):
√D2+d2−D=λ2
- Rearranging gives:
√D2+d2=D+λ2
4. Squaring Both Sides:
- Squaring both sides:
D2+d2=(D+λ2)2
- Expanding the right side:
D2+d2=D2+λD+λ24
- Canceling D2 from both sides:
d2=λD+λ24
5. Solving for D:
- Rearranging gives:
D=d2−λ24λ
6. Substituting Values:
- Convert d to meters:
d=1.0×10−4 m,λ=600×10−9 m
- Plugging in the values:
D=(1.0×10−4)2−(600×10−9)24600×10−9
7. Calculating:
- Calculate D:
D=1.0×10−8−3.6×10−134600×10−9
D=1.0×10−8−9.0×10−14600×10−9≈1.0×10−8600×10−9≈16.67 m
Summary for Part (b):
- The position of the farthest minimum detector is approximately D≈16.67 m.
---
- We have two sources, S1 and S2, separated by a distance d=1.0×10−2 cm.
- The wavelength of the light emitted by these sources is λ=600 nm (which is 600×10−9 m).
- A detector moves along the line S1P, which is perpendicular to the line S1S2.
- The minimum path difference occurs when the detector is positioned such that the light from both sources reaches it at the same time.
- This happens when the detector is very far away from the sources, ideally at infinity, or when it is directly in line with S1.
- Therefore, the minimum path difference is Δxmin=0.
- The maximum path difference occurs when the detector is positioned such that the distance from S2 to the detector is maximized.
- This happens when the detector is directly in line with S2 (i.e., at point S2).
- The path difference in this case is equal to the distance between the two sources, which is Δxmax=d.
- Convert d from cm to meters:
d=1.0×10−2 cm=1.0×10−4 m
- Thus, the maximum path difference is:
Δxmax=1.0×10−4 m
- Minimum Path Difference: Δxmin=0
- Maximum Path Difference: Δxmax=1.0×10−4 m
- For destructive interference (minima), the path difference must be an odd multiple of half the wavelength:
Δx=(m+12)λ(m=0,1,2,…)
- Let D be the distance from S1 to the detector along the line S1P.
- The path lengths from S1 and S2 to the detector can be calculated using the Pythagorean theorem:
S1P=D,S2P=√D2+d2
- The path difference is given by:
Δx=S2P−S1P=√D2+d2−D
- For the first minimum (m=0):
√D2+d2−D=λ2
- Rearranging gives:
√D2+d2=D+λ2
- Squaring both sides:
D2+d2=(D+λ2)2
- Expanding the right side:
D2+d2=D2+λD+λ24
- Canceling D2 from both sides:
d2=λD+λ24
- Rearranging gives:
D=d2−λ24λ
- Convert d to meters:
d=1.0×10−4 m,λ=600×10−9 m
- Plugging in the values:
D=(1.0×10−4)2−(600×10−9)24600×10−9
- Calculate D:
D=1.0×10−8−3.6×10−134600×10−9
D=1.0×10−8−9.0×10−14600×10−9≈1.0×10−8600×10−9≈16.67 m
- The position of the farthest minimum detector is approximately D≈16.67 m.
Topper's Solved these Questions
- LIGHT WAVESBOOK - HC VERMACHAPTER - LIGHT WAVESEXERCISE - Short Answer
11 Videos
- LIGHT WAVESBOOK - HC VERMACHAPTER - LIGHT WAVESEXERCISE - Objective 1
17 Videos
- LIGHT WAVESBOOK - HC VERMACHAPTER - LIGHT WAVESEXERCISE - Exercises
41 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMACHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercises
79 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
Similar Questions
Two sources S1 and S2 emitting light of wavelength 600 nm placed a distance 1.0×10−2 cm apart.
A detector can be moved on line S1P which is perpendicular to S1S2
(a) What would be the minimum and maximum path difference at the detector as it moves along line S1P ?
(b) Locate the position of the farthest minima detected
 .
.
View SolutionTwo sources S1 and S2 emitting light of wave lengths 600 nm are placed a distance 1.0 x 102 cm apart..A detector can be moved on the line which is perpendicular to SiS2 . Find out the position of first.minimum detected.
View Solution
Knowledge Check
Two coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .A7λ12B15λ4Cλ2D3λ4
.A7λ12B15λ4Cλ2D3λ4While conduction the Young's double slit experiment, a student replaced the two slits with a large opaque plate in the x-y plane containing two small holes that act as two coherent point sources (S1,S2) emitting light of wavelength 600nm. The student mistakenly placed the screen parallel to the x-z plane (forz>0) at a distance D=3 m from the mid-point of S1,S2, as shown schematically in the figure. The distance between the sources d=0.6003mm. The origin O is at the intersection of the screen and the line joining S1S2. Which of the following is (are) true of the intensity pattern of the screen?
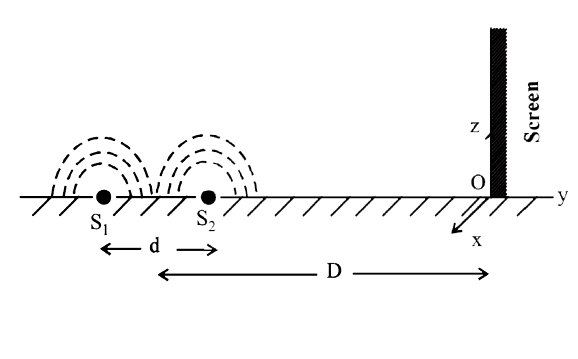 AStraight bright and dark bands parallel to the x-axisBThe region very close to the point O will be darkCHyperbolic bright and dark bands with foci symmetrically placed about O in the x-directionDSemi circular bright and dark bands centered at point.
AStraight bright and dark bands parallel to the x-axisBThe region very close to the point O will be darkCHyperbolic bright and dark bands with foci symmetrically placed about O in the x-directionDSemi circular bright and dark bands centered at point.
S1andS2 are two sources of light separated by a distance d. A detector can move along S2 P perpendicular to S1S2. What should be the minimum and maximum path difference at the detector?

View SolutionTwo sources of sound, S1andS2 , emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S_1S_2 and at a distance of 20.0 cm from P it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in phase, find the minimum distance through wffich the detector should be shifted to detect a minimum of sound.
View SolutionTwo source of sound, S1 and S2, emitting waves of equal wavelength 2cm, are placed with a separation of 3cm between them. A detector can be moved on a line parallel to S1S2 and at a distance 24cm from it. Initially, the detecor is equidistant from the two sources. Assuming that the waves emitted by the sources are in phase, find the minimum distance through which the detector should be shifted to detect a minimum of sound.
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S1 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O

View SolutionTwo coherent sources Sf and S2 (in phase with ech other) are placed at a distance of 2λ as shown where λ is wavelength of sound. A detector moves on line AB parrallel to S1S2. If detector detects maximum intensity at finite distance from O at θ=±(πn). Find n

View Solution
