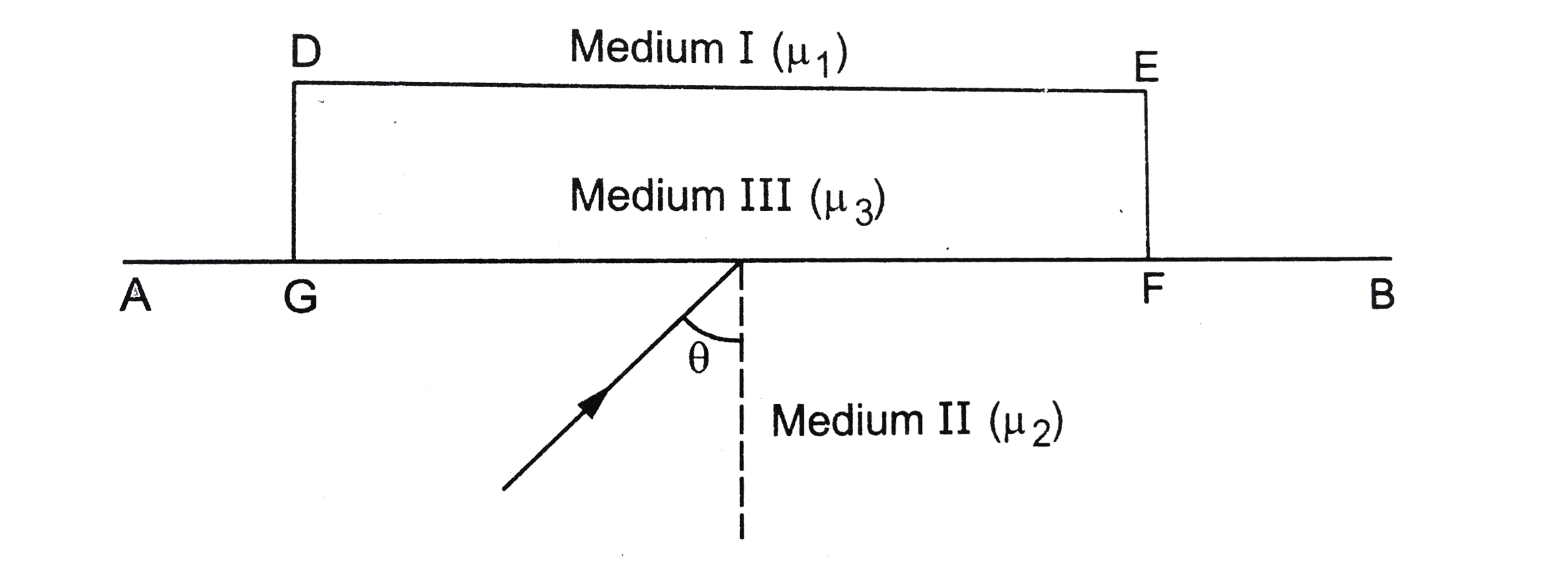
Monochramatic light is incident on the pane interface AB between two media of refractive indices and at an angle of incidence theta as shown in figure. The angle theta is infinitesimally greater thannte critical angle for the two media so thast total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive inde is introduced on theinterface (as shown in figure ) , show that for any value of all light will ultimately be reflected back into medium II.
We shall use the symbol to mean infinitesimaly greater than. ltbr> When the slab is not inserted
or .
When the slab is inserted. We have two cases .
Case I: mu_2lemu_1
thus, the light is incident on AB at an angle greater than the criticle angle mu_3gtmu_1sintheta bargt mu_1/mu_2ltmu_3/mu_2sin^-1 (mu_3/mu_2)(sintheta)/(sintheta')=mu_3/mu_2or sintheta'=mu_2/mu_3sinthetabargtmu_2/mu_3.mu_1/mu_2
Similar Questions
A monochromatic light is incident on the plane interface AB between two media of refractive indices μ1 and (μ2>μ1) at an angle of incidence θ as shown in Fig.
The angle θ is infinitesimally greater than the critical angle for the two media so that total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive index μ3 is introduced on the interface (as shown in the figure), show that for any value of μ3 all light will ultimately be reflected back into medium II.

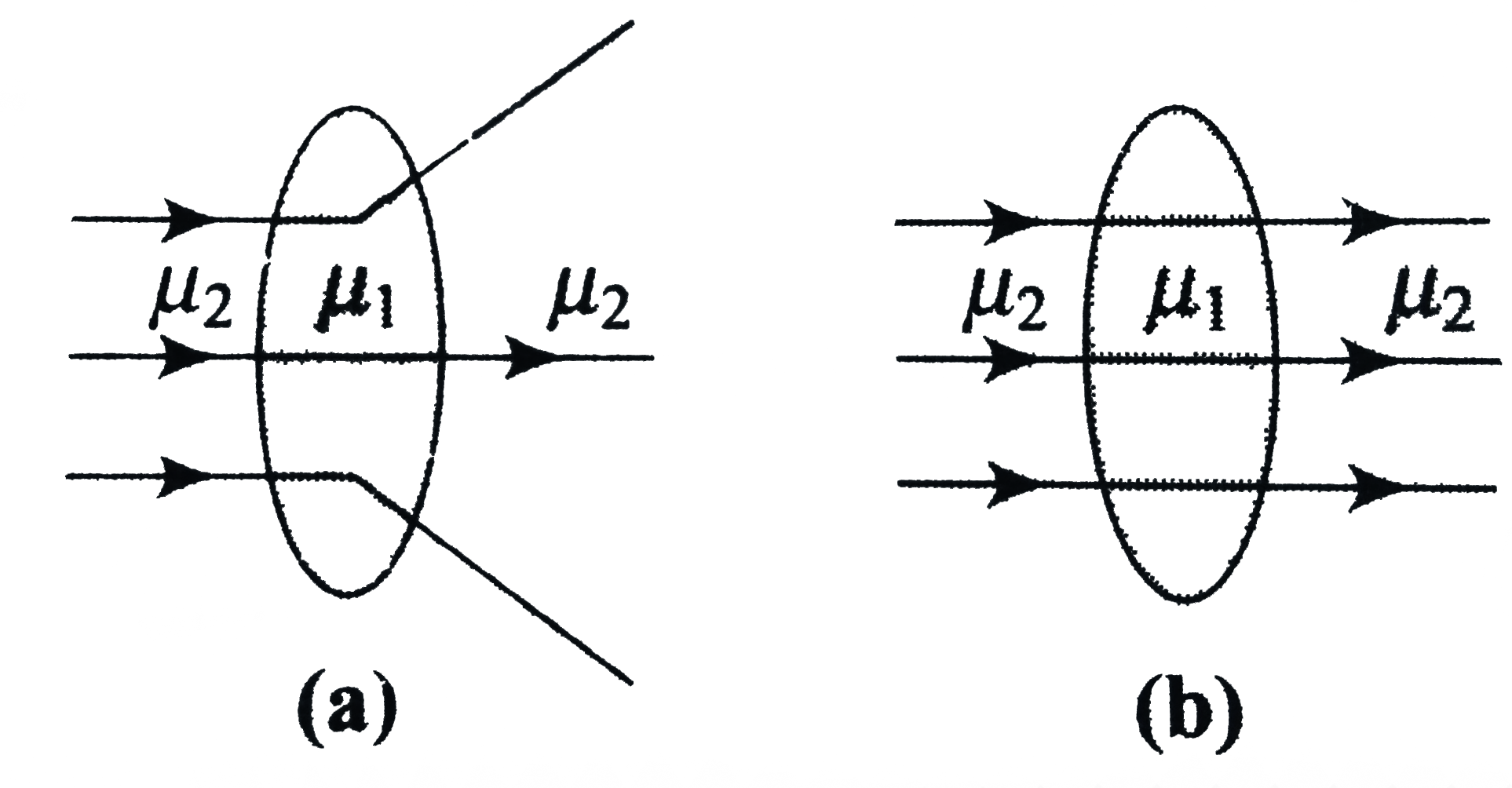
View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
View Solution
Knowledge Check
The relation between refractive indices u,μ1,μ2. if the behaviour of light ray is as shown in figure
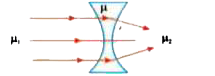 Aμ>μ1>μ2Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2
Aμ>μ1>μ2Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2Two optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
A(x−y)xB(x+y)xCxy−xDyxTwo optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
Ax−yxB(x+Y)xCxy−xDyx
A light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
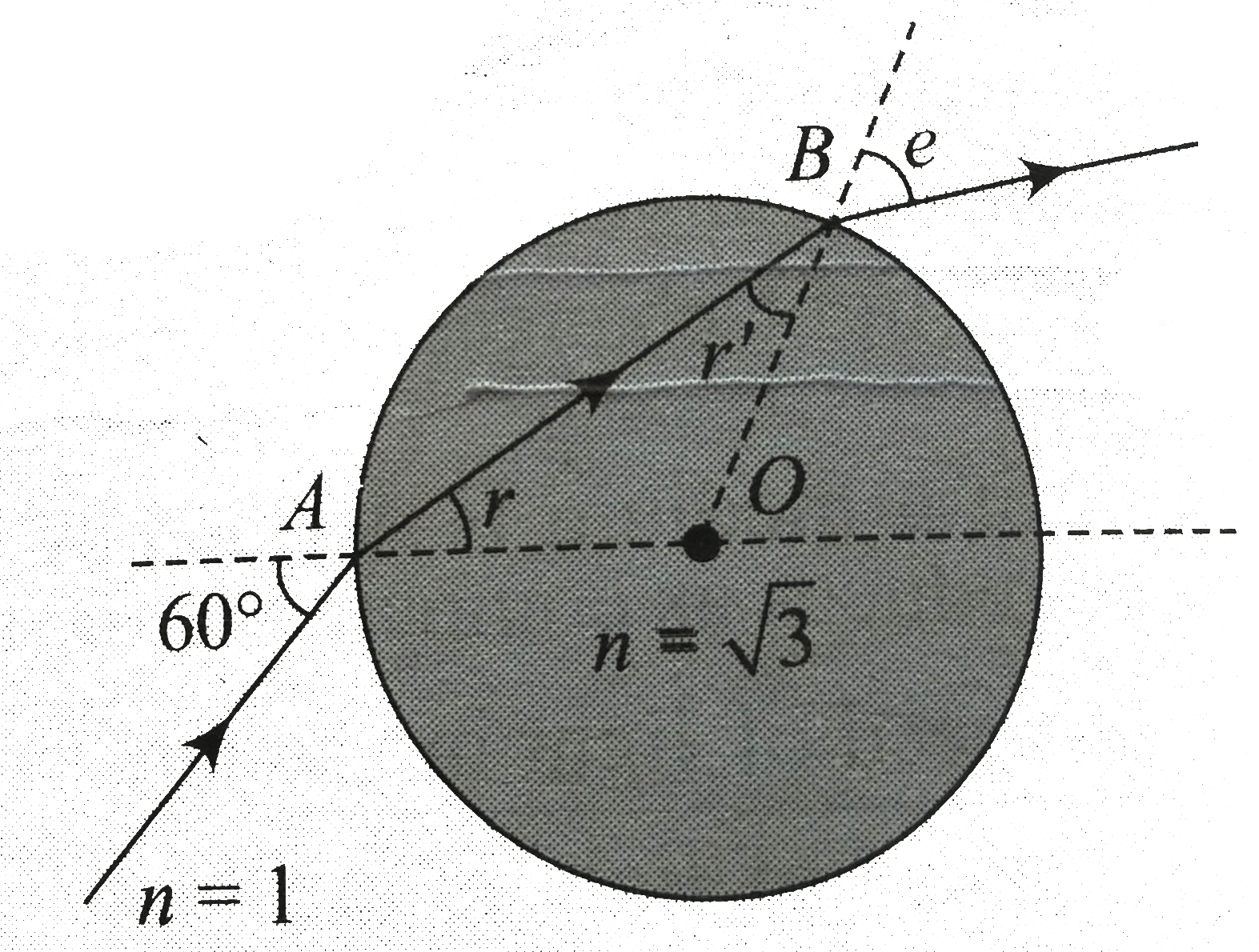
View SolutionFor total internal reflection to take place, the angle of incidence I and the refractive index μ of the medium must satisfy the inequality
View SolutionFor total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
View SolutionIn total internal reflection when the angle of incidence is equal to the critical angle for the pair of media in contact, what will be angle of refraction?
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
View Solution
