If $\to A = \to B + \to C$ , and the magnitudes of $\to A$ , $\to B$ , $\to C$ are 5,4, and 3 units, then the angle between $\to A$ and $\to C$ is

A

${cos}^{- 1} (3 / 5)$

B

${cos}^{- 1} (4 / 5)$

C

$π / 2$

D

${sin}^{- 1} (3 / 4)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

See the vector diagam given below OR =5 units
OP=4 units, OQ=3 units

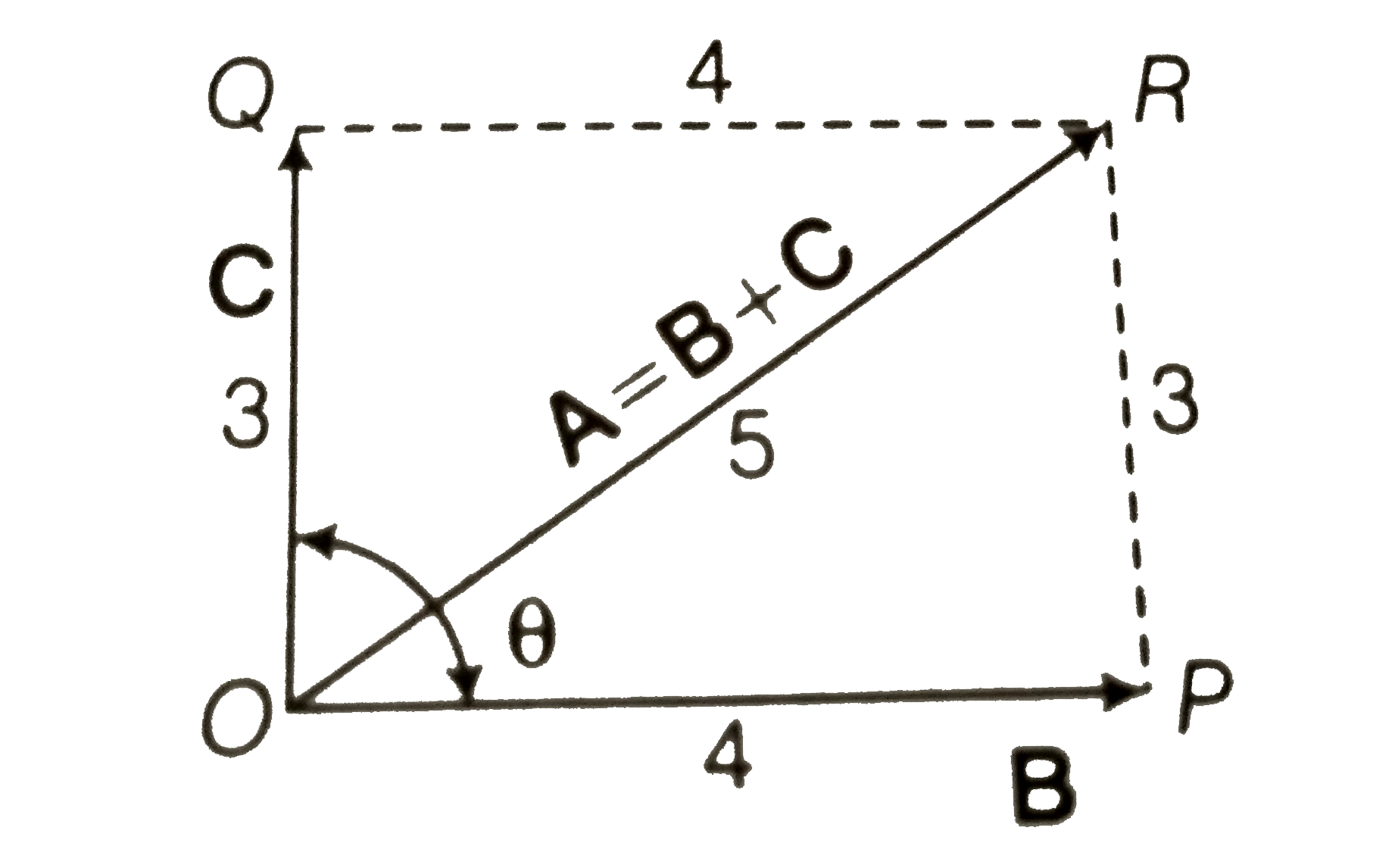
As,
$5 = \sqrt{4^{2} + 3^{2} + 2 \times 4 \times 3 \times cos θ}$
Taking square on both sides
$\Rightarrow 25 = 16 + 9 + 24 cos θ$
$\Rightarrow cos θ = 0 \Rightarrow 90^{\circ} = \frac{π}{2}$
Angle betwen A and C $= ∠ Q O R$
$sin (∠ Q O R) = \frac{4}{5}$
$\Rightarrow ∠ Q O R = {sin}^{- 1} (\frac{4}{5})$
Also, $cos (∠ Q O R) = \frac{3}{5}$
$\Rightarrow ∠ Q O R = {cos}^{- 1} (\frac{3}{5})$

|

Updated on:21/07/2023

Class 12 PHYSICS PRACTICE SET 07

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $\to A = \to B + \to C$ and the magnitude of $\to A, \to B and \to C$ are 5, 4, and 3 units respectively the angle between $\to A and \to B$ is :
A ${cos}^{- 1} (\frac{3}{5})$
B ${cos}^{- 1} (\frac{4}{5})$
C $(\frac{π}{2})$
D ${sin}^{- 1} (\frac{4}{5})$
Question 2 - Select One
If $\to A + \to B = \to C$ and $A + B = C$ , then the angle between $\to A$ and $\to B$ is :
A0
B $\frac{π}{4}$
C $\frac{π}{2}$
D $π$
Question 3 - Select One
The magnitude of vector $\to A, \to B$ and $\to C$ are respectively 12,5 and 13 unit and $\to A + \to B = \to C$ then the angle between $\to A$ and $\to B$ is
A0
B $π$
C $π / 2$
D $π / 4$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-PRACTICE SET 07-PAPER 1( PHYSICS & CHEMISTRY)

Home
Ask Doubt
Profile