Two plane mirros are inclined at an anle θ. It is found that a ray incident on one mirror at any angle is rendered paralle ot itself after reflection from both the mirrors. The value of θ is
30∘
60∘
90∘
120∘
The correct Answer is:C
To solve the problem, we need to determine the angle θ between two plane mirrors such that a ray incident on one mirror at any angle is rendered parallel to itself after reflection from both mirrors.
1. Understanding the Problem:
- We have two plane mirrors inclined at an angle θ.
- A ray of light strikes one of the mirrors and after reflecting from both mirrors, it emerges parallel to its original direction.
2. Concept of Deviation:
- When a ray of light reflects off a mirror, it undergoes a deviation. For two mirrors inclined at an angle θ, the total deviation δ of the ray after reflecting off both mirrors is given by:
δ=2θ
- This means that the ray is effectively rotated by an angle of 2θ.
3. Condition for Parallelism:
- For the ray to emerge parallel to its original direction, the total deviation must be equal to 180∘ (i.e., the ray is turned halfway around).
- Therefore, we set up the equation:
2θ=180∘
4. Solving for θ:
- Dividing both sides of the equation by 2 gives:
θ=180∘2=90∘
5. Conclusion:
- The angle θ between the two mirrors must be 90∘ for the ray to emerge parallel to itself after reflection.
Final Answer:
The value of θ is 90∘.
---
- We have two plane mirrors inclined at an angle θ.
- A ray of light strikes one of the mirrors and after reflecting from both mirrors, it emerges parallel to its original direction.
- When a ray of light reflects off a mirror, it undergoes a deviation. For two mirrors inclined at an angle θ, the total deviation δ of the ray after reflecting off both mirrors is given by:
δ=2θ
- This means that the ray is effectively rotated by an angle of 2θ.
- For the ray to emerge parallel to its original direction, the total deviation must be equal to 180∘ (i.e., the ray is turned halfway around).
- Therefore, we set up the equation:
2θ=180∘
- Dividing both sides of the equation by 2 gives:
θ=180∘2=90∘
- The angle θ between the two mirrors must be 90∘ for the ray to emerge parallel to itself after reflection.
The value of θ is 90∘.
Topper's Solved these Questions
Similar Questions
Two plane mirrors are inclined at angleθ.A ray of light is incident on one mirror at an angle of incidence.i.The rayis refelected from this mirror,falls on the second mirror from where it is refleced parallel to the first mirror .What is the value of i,the angle of incident in term of θ?
View SolutionTwo plane mirrors are placed at an angle θso that a ray parallel to one mirror gets reflected parallel to second mirror after two consecutive reflections .The value of θwill be-
View Solution
Knowledge Check
Two plane mirrors are inclined at an angle 1θ . If is found that a ray incident on one mirror at any angle is rendered parallel to itself after reflection from both the mirrors. The value of 1θ is
A30∘B60∘C90∘D120∘Two plane mirrors are inclined at an angle 1θ . If is found that a ray incident on one mirror at any angle is rendered parallel to itself after reflection from both the mirrors. The value of 1θ is
A30∘B60∘C90∘D120∘Two plane mirrors are inclined at an angle θ to one another A ray of light incident on the first mirror and parallel ot the second mirror is reflected from the second mirror parallel to the first mirror ,
What is the value of θA0∘B45∘C60∘D90∘
Two plane mirrors are inclined at an angle θ . A light ray incident on one of the mirrors undergoes multiple reflections. The angle of incidence on the first mirror is 15∘ . After reflection from the second mirror, if the light ray retraces its path, determine the value of θ.
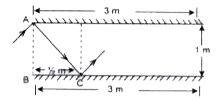
View SolutionTwo plane mirrors are inclined to each other such that a ray of light incident on the first mirror and parallel to the second is reflected from the second mirror parallel to the first mirror. Determine the angle between the two mirrors:
View SolutionTwo plane mirrors are inclined at 70∘. A ray incident on one mirror at incidence angle θ after reflection falls on the second mirror and is reflected from there parallel to the first mirror, The value of θ is
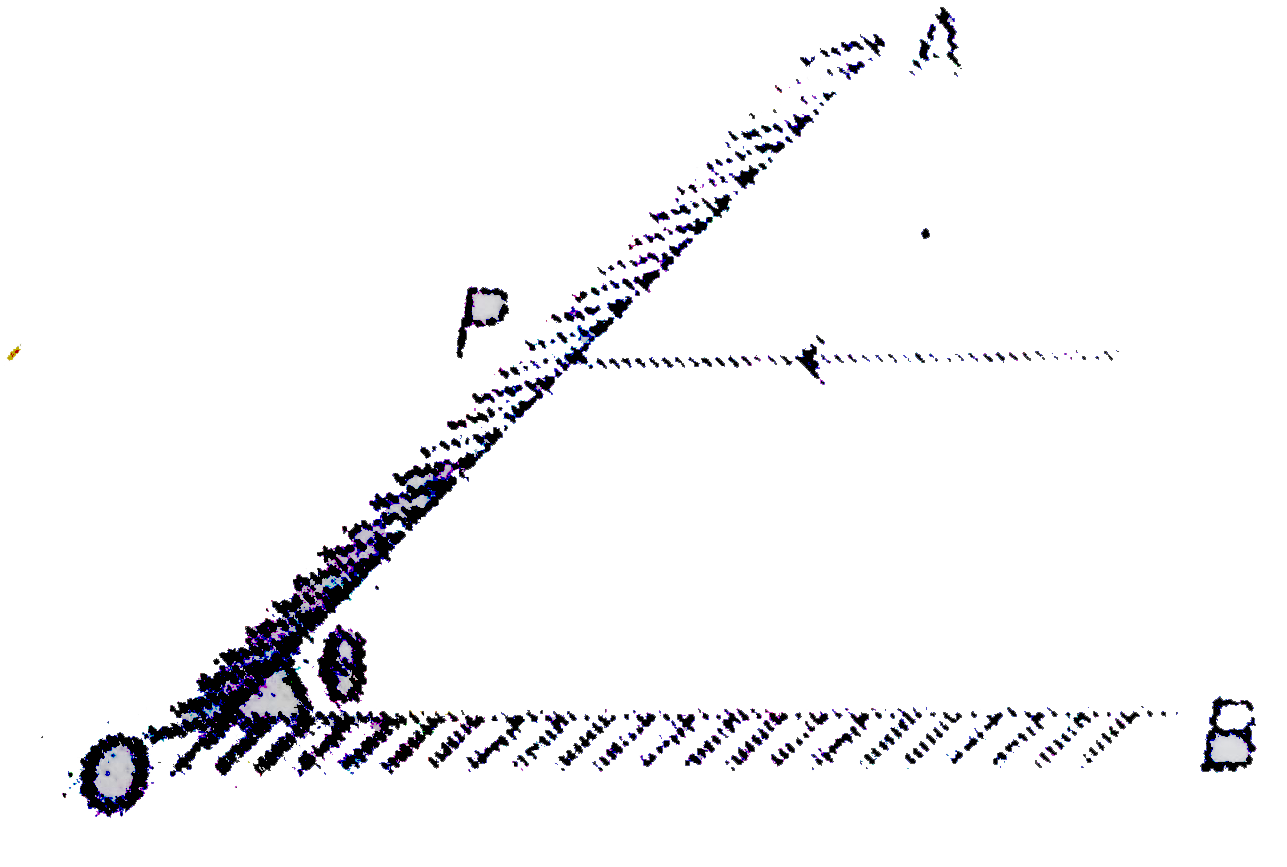
View SolutionTwo plane mirrors are inclined at angle θ as shown in figure. If a ray parallel to OB strikes the other mirror at P and finally emerges parallel to OA after two reflections then θ is equal to
View SolutionTwo plane mirrors are inclined to each other such that a ray of light incident on the first mirror and parallel to the second is reflected from the second mirror parallel to the first mirror. The angle between the two mirrors is :
View Solution
