Find the area bounded by the curves x2+y2=25,4y=∣∣4−x2∣∣, and x=0 above the x-axis.
A
4+25sin−1(4/5)
B
12{8−25sin−1(4/5)}
C
14{425sin−1(4/5)}
D
None of these
Video Solution
Text Solution
The correct Answer is:C
4y=∣∣4−x2∣∣.x≥0
⇒{4y=4−x2:0≤x≤24y=x2−4:x≥2
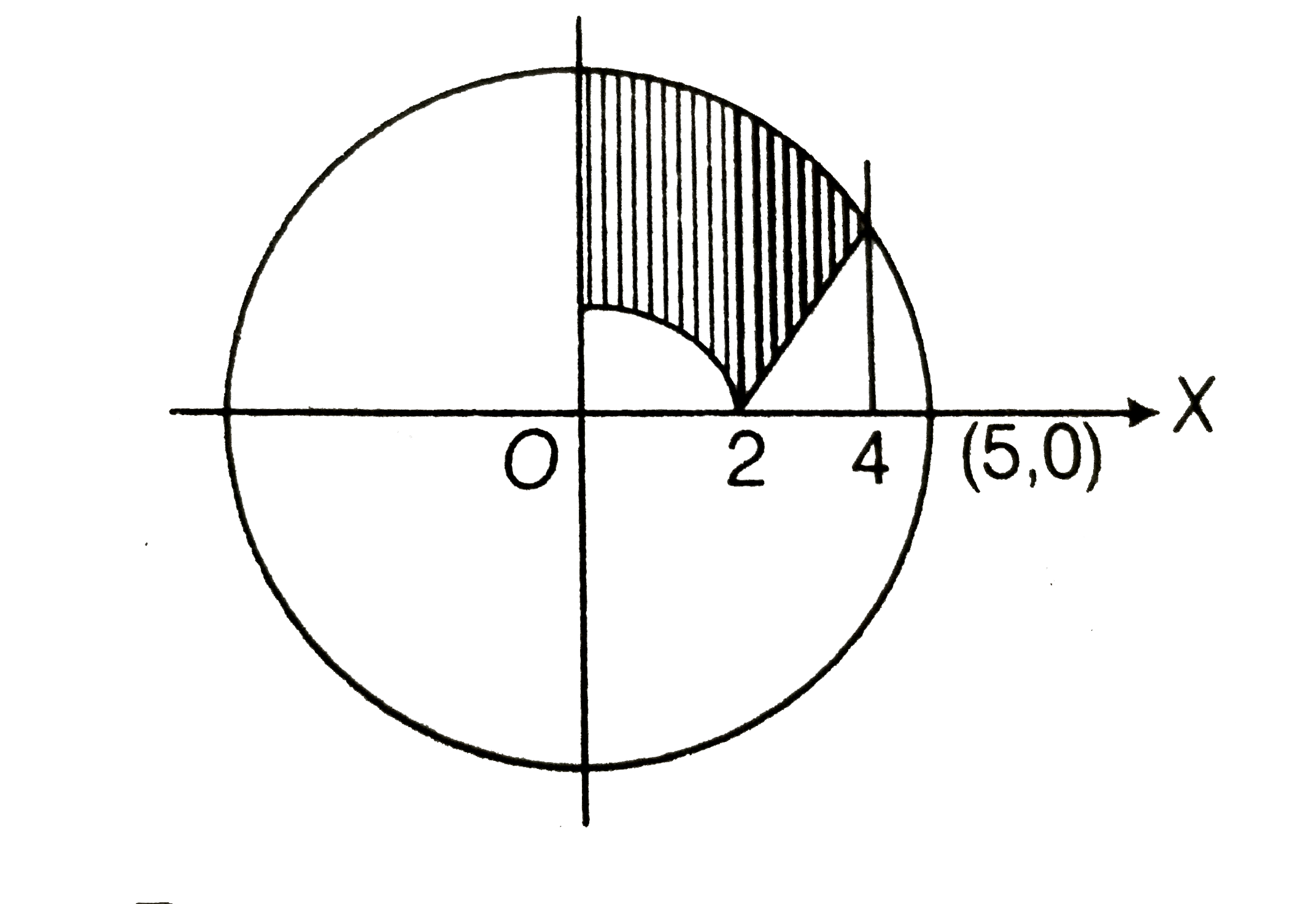
Region bounded by the curves
x2+y2=25
4y=∣∣4−x2∣∣,x≥0,y>0 is shaded
Solving x2=4(y+1)andx2+y2=25 we, get
y2+4y−21=0
⇒y=3
⇒x=4
Required area
∫20(√25−x2−14(4−x2))dx
+∫42(√25−x2−14(x2−4))dx
=12(4+25+sin−1(4/5))
|
Topper's Solved these Questions
Similar Questions
Find the area bounded by the curves x2+y2=25,4y=∣∣4−x2∣∣, and x=0 above the x-axis.
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0 .
View SolutionFind the area bounded by the curves 4y=∣∣4−x2∣∣,y=7−|x|
View SolutionFind the area bounded by the curves : y2=4x,y2=x,x=1andx=4
View SolutionFind the area bounded by the curve y=−3|x|+2 and x-axis
View Solution.Find the area bounded between the curves y2=4x,y2=4(4−x)
View SolutionFind the area bounded by the curve 4y2=9xand3x2=16y
View SolutionFind the area bounded by the curves x2=y, x2=−y and y2=4x−3
View SolutionFind the area bounded by the curve y2=4ax and x2+y2−2ax=0 above the x-axis.
View SolutionFind the area bounded by the curves x2+y2=4 and x2+y2=4x
View Solution
