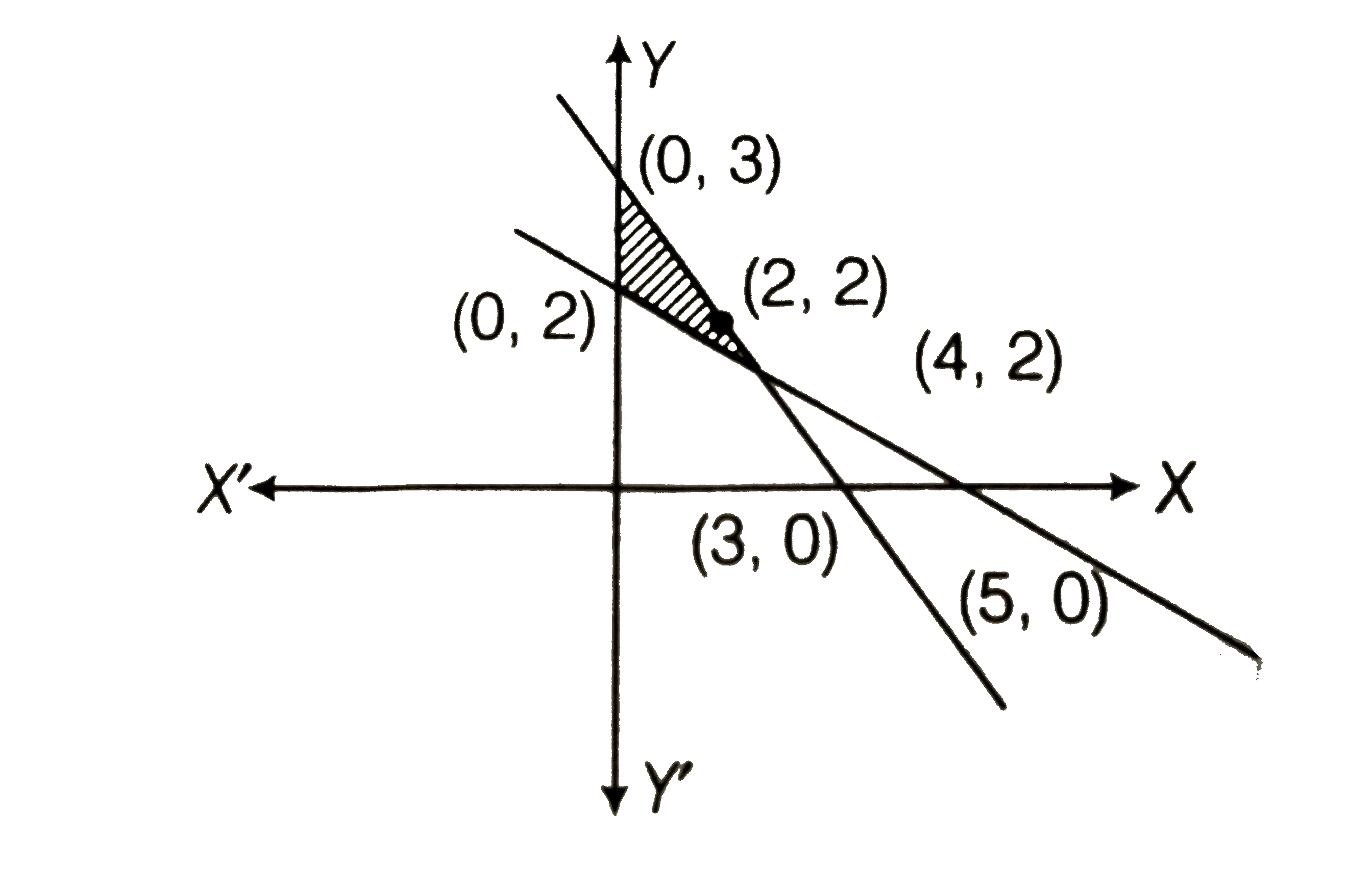
Consider the inequalities x1+x2≤,2,2x1+5x2≥10,x1,x2≥0. Which of the following point lie in the fesible region ?
(2,2)
(1,2)
(2,1)
(4,2)
The correct Answer is:C
It is clear from the figure that points (2,2) (4,2) and (2,1) lies outside the fesible be region lies outside the fesible be region and only the points (1,2) lies in the fesible region.
Topper's Solved these Questions
Similar Questions
If 3x+4y≥12,2x+y≤6,x≥0,y≥0, then the corner points of the feasible region are
View Solution(a) Draw the feasible region of inequation:
x+y≤4,x≥0,y≥0
(b) Draw the graph of the following LPP:
3x+y≤17,x,y≥0
(c) Shade the feasible region of LLP:
(i) x+3y≥3,x+y≥2,x≥0,y≥0
(ii) x+2y≤8,3x+2y≤12,x≥0,y≥0View Solution
Knowledge Check
- Question 1 - Select One
Consider the inequalities x1+x2≤3,2x1+5x2≥10x1,x2≥0 which of the following point does not lie in the feasible region ?
A(2, 2)B(1, 2)C(2, 1)D(4, 2) - Question 2 - Select One
Consider the inequalities 5x1+4x2≥9,x1x2≥3, x1>0,x2>0. Which of the following point does not lie inside the solution set ?
A(1,3)B(1,2)C(1,4)D(1,1) - Question 3 - Select One
Consider the inequalities 5x1+4x2≥9,x1+x2≤3,x1≥0,x2≥0 Which of the following point lies inside the solution set ?
A(1,3)B(1,2)C(1,4)D(2,2)
Solution set of the inequalities x+2y≥11,3x+4y≤30,2x+5y≤30,x≥0,y≥0 includes the point
View SolutionConsider the inequalities x1+x2≤3,2x1+5x2≥10x1,x2≥0 then feasible region is
View SolutionThe objective function Z=x1+x2, subject to x1+x2≤10,−2x1+3x2≤15,xx1≤6,x1,x2≥0 has maximum value ________ of the feasible region .
View SolutionIf 3x1+5x2≤15,5x1+2x2≤10,x1,x2≥0, then the maximum value of z=5x1+3x2 by graphical method is
View SolutionFor the LPP Min z=x1+x2 such that inequalities
5x1+10x2≥0,x1+x2≤1,x2≤4 and x−1,x2≥0View Solution

