A body of mass m is travelling with a velocity vu. When a constant retarding force F is applied, it comes to rest after travelling a distance s1. If the initial velocity is 2u with the same force F, the distance travelled before it comes to rest is s2. then,
s2=4s1
2s2=2s1
s2=s12
s2=s1
The correct Answer is:A
To solve the problem, we need to analyze the motion of the body under the influence of a constant retarding force. We will use the kinematic equations of motion to find the relationship between the distances s1 and s2.
1. Identify the Variables:
- Mass of the body: m
- Initial velocity in the first case: v1=u
- Initial velocity in the second case: v2=2u
- Retarding force: F
- Distance travelled in the first case: s1
- Distance travelled in the second case: s2
- Final velocity in both cases: v=0
2. Apply the Kinematic Equation for the First Case:
We can use the equation:
v2=u2+2as
For the first case:
- Final velocity v=0
- Initial velocity u=u
- Distance s=s1
- Acceleration a=−Fm (negative because it's a retarding force)
Plugging these into the equation:
0=u2+2(−Fm)s1
Rearranging gives:
u2=2Fms1(1)
3. Apply the Kinematic Equation for the Second Case:
For the second case:
- Final velocity v=0
- Initial velocity u=2u
- Distance s=s2
- Acceleration a=−Fm
Using the same kinematic equation:
0=(2u)2+2(−Fm)s2
Rearranging gives:
4u2=2Fms2(2)
4. Relate the Two Equations:
From equation (1):
s1=mu22F(3)
From equation (2):
s2=4mu22F=2mu2F(4)
5. Find the Relationship Between s1 and s2:
Now, substituting equation (3) into equation (4):
s2=4s1
Final Result:
Thus, the relationship between s1 and s2 is:
s2=4s1
- Mass of the body: m
- Initial velocity in the first case: v1=u
- Initial velocity in the second case: v2=2u
- Retarding force: F
- Distance travelled in the first case: s1
- Distance travelled in the second case: s2
- Final velocity in both cases: v=0
We can use the equation:
v2=u2+2as
For the first case:
- Final velocity v=0
- Initial velocity u=u
- Distance s=s1
- Acceleration a=−Fm (negative because it's a retarding force)
0=u2+2(−Fm)s1
Rearranging gives:
u2=2Fms1(1)
For the second case:
- Final velocity v=0
- Initial velocity u=2u
- Distance s=s2
- Acceleration a=−Fm
0=(2u)2+2(−Fm)s2
Rearranging gives:
4u2=2Fms2(2)
From equation (1):
s1=mu22F(3)
From equation (2):
s2=4mu22F=2mu2F(4)
Now, substituting equation (3) into equation (4):
s2=4s1
Thus, the relationship between s1 and s2 is:
s2=4s1
Topper's Solved these Questions
Similar Questions
A stone of mass 1 kg is thrown with a velocity of 20 m/s across the frozen surface of a take and it comes to rest after travelling a distance of 50 m . What is the magnitude of the force opposing the motion of the stone ?
View SolutionA stone of 1 kg is thrown with a velocity of 20ms−1 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice?
View Solution
Knowledge Check
- Question 1 - Select One
A stone of mass 1 kg is thrown with a velocity of 20ms−1 across the frozen surface of a lake and it comes to rest after travelling a distance of 50m. What is the magnitude of the force opposing the motion of the stone?
A−2NB−1NC−3ND−4N - Question 2 - Select One
If S=16+(192)t−t3, then distance travelled by the particle before coming to rest is
A1040 unitsB520 unitsC260 unitsD2080 units - Question 3 - Select One
Initially a car is moving with speed of 20ms−1 and covers a distance of 100 m before it comes to rest. On making the initial speed of car 40ms−1 keeping the acceleration same, the distance travelled by car before it comes to rest is
A200 mB300 mC400 mD800 m
A stone of 1kg is thrown with a velocity of 20ms−1 across the frozen surface of lake and comes to rest after travelling a distance of 50m. What is the force of friction between the stone and the ice?
View SolutionA stone of 1 kg is thrown with a velocity of 20ms−1 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice ?
View SolutionA body of mass 3 kg travelling with a velocity 5m/s collides head - on and elastically with a body of mass 2kg travelling at a speed 5m/s in opposite direction.The velocity of the second body after the collision is?
View SolutionThe figure-1.125 shows the acceleration versus time graph of a train. If it starts from rest, the distance it travels before it comes to rest is :
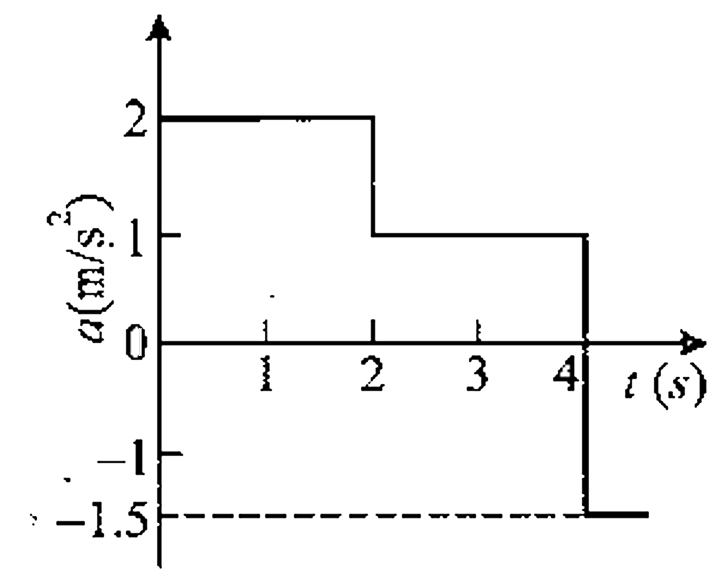 View Solution
View SolutionIf S=13t3−4t2+12t, then distance travelled by the particle before it first comes to rest is
View Solution

