A uniform disc of radius R lies in xy-plane with its centre at origin. Its moments of inertia about the axis X=2R and Y=0 is equal to the moment of inertia about the axis Y=d and Z=0. What is the value of d?
√172R
√13R
√152R
43R
The correct Answer is:A
To solve the problem, we need to find the value of d such that the moment of inertia of a uniform disc about two different axes is equal. We will use the parallel axis theorem to compute the moments of inertia about the specified axes.
1. Identify the Moments of Inertia:
- The moment of inertia I of a uniform disc about an axis perpendicular to its plane through its center is given by:
ICM=12mR2
where m is the mass of the disc and R is its radius.
2. Moment of Inertia about Axis 1 (X = 2R, Y = 0):
- We will use the parallel axis theorem to find the moment of inertia about the axis at x=2R.
- According to the parallel axis theorem:
I1=ICM+md2
where d is the distance from the center of mass to the new axis. Here, the distance d is 2R.
- Therefore:
I1=12mR2+m(2R)2
I1=12mR2+4mR2=12mR2+8mR2=172mR2
3. Moment of Inertia about Axis 2 (Y = d, Z = 0):
- Now, we find the moment of inertia about the axis at y=d.
- Again, using the parallel axis theorem:
I2=ICM+md2
- Here, the distance d is d itself (the distance from the center of mass to the new axis):
I2=12mR2+md2
4. Setting the Moments of Inertia Equal:
- According to the problem, I1=I2:
172mR2=12mR2+md2
- We can cancel m from both sides (assuming m≠0):
172R2=12R2+d2
5. Solving for d2:
- Rearranging the equation gives:
d2=172R2−12R2
d2=17−12R2=162R2=8R2
6. Finding d:
- Taking the square root of both sides:
d=√8R=2√2R
Final Answer:
Thus, the value of d is:
d=2√2R
- The moment of inertia I of a uniform disc about an axis perpendicular to its plane through its center is given by:
ICM=12mR2
where m is the mass of the disc and R is its radius.
- We will use the parallel axis theorem to find the moment of inertia about the axis at x=2R.
- According to the parallel axis theorem:
I1=ICM+md2
where d is the distance from the center of mass to the new axis. Here, the distance d is 2R.
- Therefore:
I1=12mR2+m(2R)2
I1=12mR2+4mR2=12mR2+8mR2=172mR2
- Now, we find the moment of inertia about the axis at y=d.
- Again, using the parallel axis theorem:
I2=ICM+md2
- Here, the distance d is d itself (the distance from the center of mass to the new axis):
I2=12mR2+md2
- According to the problem, I1=I2:
172mR2=12mR2+md2
- We can cancel m from both sides (assuming m≠0):
172R2=12R2+d2
- Rearranging the equation gives:
d2=172R2−12R2
d2=17−12R2=162R2=8R2
- Taking the square root of both sides:
d=√8R=2√2R
Thus, the value of d is:
d=2√2R
Topper's Solved these Questions
Similar Questions
Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View SolutionA uniform circular disc of radius R lies in the XY plane with its centre coinciding with the origin.The moment of inertia about an axis passing through a point on the X-axis at a distance x=2R and perpendicular to the X-Y plane is equal to its moment of inertia about an axis passing through a pint on the Y-axis at a distance y=d and parallel to the X-axis in the X-Y plane. The value of d is
View Solution
Knowledge Check
- Question 1 - Select One
A uniform disc of radius R lies in xy plane with its centre at origin. Its moment of inertia about the axis x = 2 R and y =0 is equal to the moment of inertia about the axis y =d and z = 0. What is d equal to ?
A√172RB√13RC√152RD43R - Question 2 - Select One
A uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
A43RB√172RC√13RD√152R - Question 3 - Select One
A uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
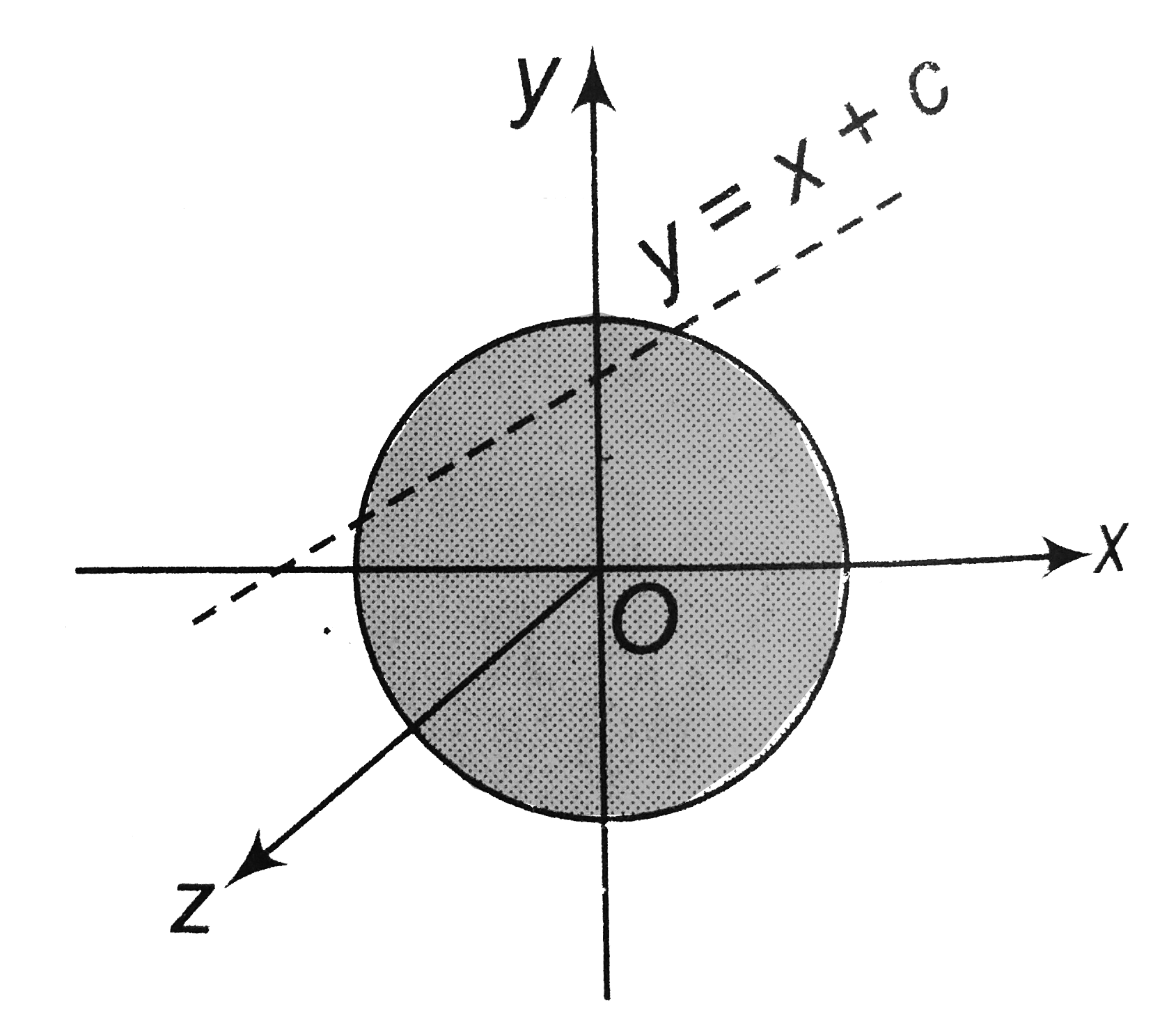 .A−R2B±R√2C+R4D−R
.A−R2B±R√2C+R4D−R
Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is
 View Solution
View SolutionA ring of radius 1m is in xy-plane with centre at the origin. In each of option below, the moment of inertia of the ring about the line is calculated. In which case does the ring have same of inertia as that about z-axis.
View SolutionThe adjoining figure shows a disc of mass M and radius R lying in the X-Y plane with its centre on X - axis at a distance a from the origin. Then the moment of inertia of the disc about the X-axis is
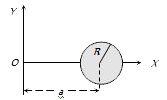 View Solution
View Solution

