If $y = f (x) and y cos x + cos y = π$ , then the value of f''(0) is

A

$π$

B

$- π$

C

0

D

$2 π$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Given, $y cos x + x cos y = π$
On differentiating both sides, we get
$\frac{d y}{d x} cos x + y (- sin x) + x (- sin y) \frac{d y}{d x} + cos y = 0$
$\Rightarrow \frac{d y}{d x} = \frac{y sin x - cos y}{cos x - x sin y}$
Again differentiating both sides, we get
$\frac{d^{2} y}{{d x}^{2}} =$

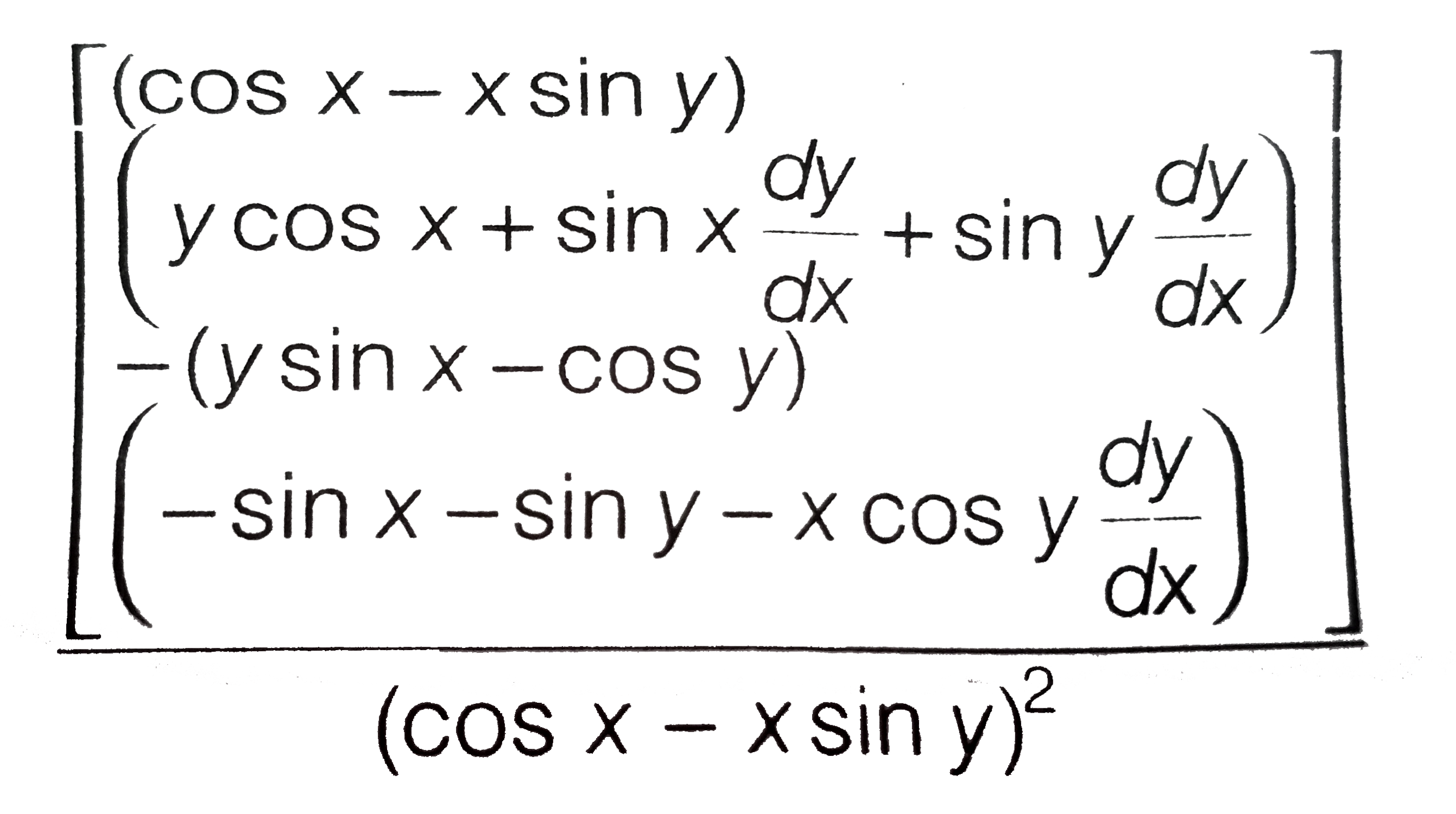
At x = 0,
$f'' (0) = \frac{1 (y + sin y) - (- 1) (- sin y)}{{(1 - 0)}^{2}} = y$
As $y cos x + x cos y = π$
$∴ At x = 0 \Rightarrow y = π$
Hence, $f'' (0) = π$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If f is a real valued function such that $f (x + y) = f (x) + f (y) and f (1) = 5$ , then the value of f(100) is
A200
B300
C400
D500
Question 2 - Select One
If $f (x) = - \int_{0}^{x} log (cos t) d t,$ then the value of $f (x) - 2 f (\frac{π}{4} + \frac{x}{2}) + 2 f (\frac{π}{4} - \frac{x}{2})$ is equal to
A $- x log 2$
B $\frac{x}{2} log 2$
C $\frac{x}{3} log 2$
DNone of these
Question 3 - Select One
If $f' (x) = {tan}^{- 1} (Sec x + tan x), x \in (- \frac{π}{2}, \frac{π}{2})$ and $f (0) = 0$ then the value of $f (1)$ is
A $\frac{π + 1}{4}$
B $\frac{π - 1}{4}$
C $\frac{π + 1}{2}$
D0

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-PRACTICE SET 14-Paper 2 (Mathematics)

Home
Ask Doubt
Profile