Find the equations of the circles touching y-axis at (0,3) and making an intercept of 8 units on the x-axis.

A

$x^{2} + y^{2} \pm 10 x - 6 y + 9 = 0$

B

$x^{2} + y^{2} \pm 6 x - 10 y + 9 = 0$

C

$x^{2} + y^{2} - 8 x \pm 10 y + 9 = 0$

D

$x^{2} + y^{2} + 10 x \pm 6 y + 9 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Given equation of circle touch the Y-axis at(0,3).
In $△ A O B, r = \sqrt{3^{2} + 4^{2}} = 5$

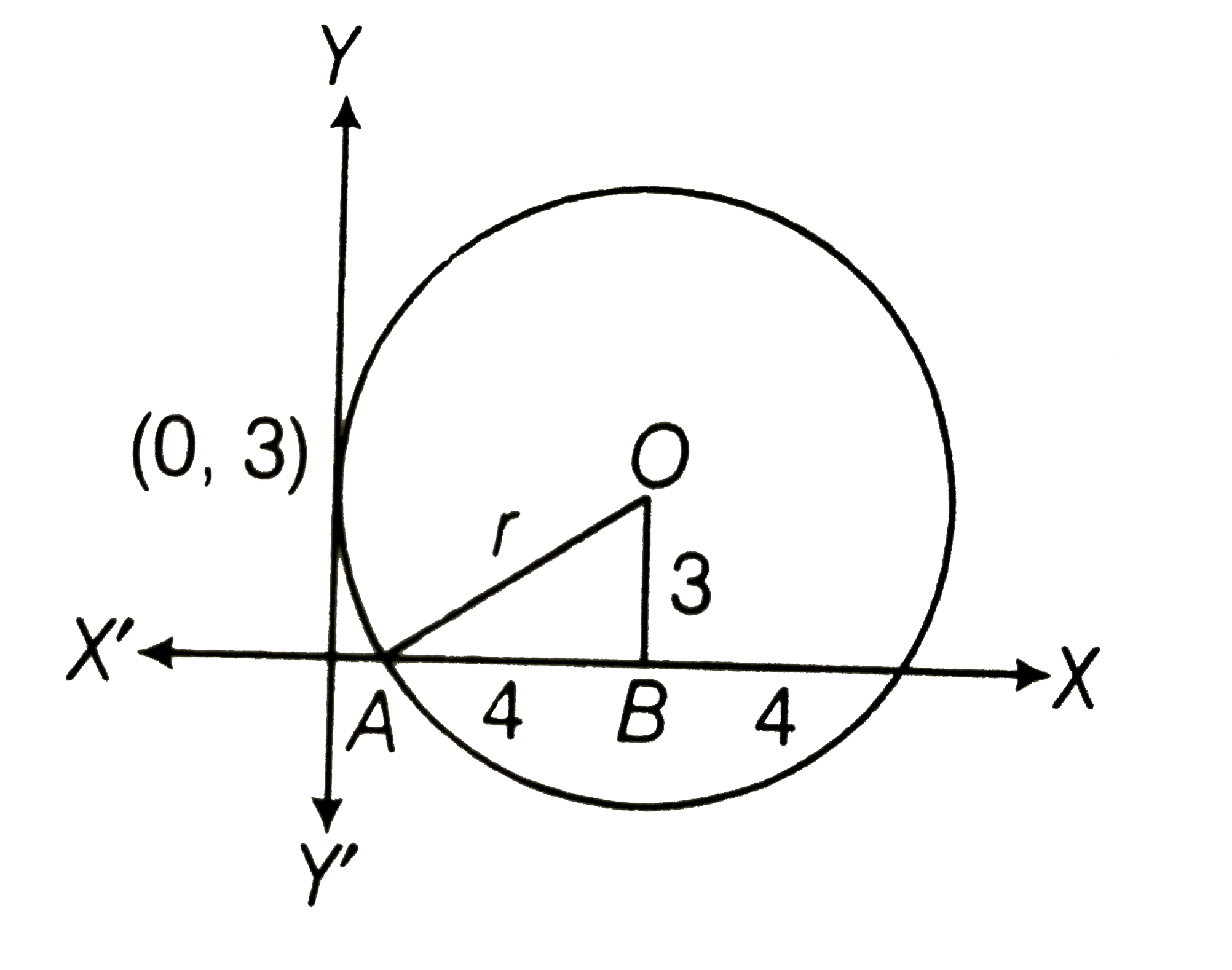
The point (0, 3) and radius 5 satisfies the equation
$x^{2} + y^{2} \pm 10 x - 6 y + 9 = 0 .$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
The equation of a circle touching x-axis at $(- 4, 0)$ and cutting off an intercept of 6 units on y-axis can be
A $x^{2} + y^{2} + 8 x + 12 y + 16 = 0$
B $x^{2} + y^{2} + 8 x - 12 y + 16 = 0$
C $x^{2} + y^{2} + 8 x + 10 y + 16 = 0$
D $x^{2} + y^{2} + 8 x - 10 y + 16 = 0$
Question 2 - Select One or More
Equations of circle which touch y-axis at (0, 3) and intercepts a length of 8 units on the x-axis is
A $x^{2} + y^{2} + 10 x - 6 y + 9 = 0$
B $x^{2} + y^{2} + 6 x - 10 y + 9 = 0$
C $x^{2} + y^{2} + 8 x + 4 y + 2 = 0$
D $x^{2} + y^{2} - 10 x - 6 y + 9 = 0$
Question 3 - Select One
Equation of a circle which touches y-axis at (0,2) and cuts ff an intercept of 3 units from the x-axis is $x^{2} + y^{2} - 2 α x - 4 y + 4 = 0$ where $α^{2} =$
A $5 / 2$
B $25 / 4$
C $4 / 25$
D $29$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-PRACTICE SET 17-MATHEMATICS

Home
Ask Doubt
Profile