If the vectors −−→AB=3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC, then the length of the median through A is (A) √33 (B) √45 (C) √18 (D) √720
√18
√72
√33
√288
The correct Answer is:C
Position vector of
AD=(3+5)ˆi+(0−2)ˆj+(4+4)ˆk2
(∵ D is mid point of BC)
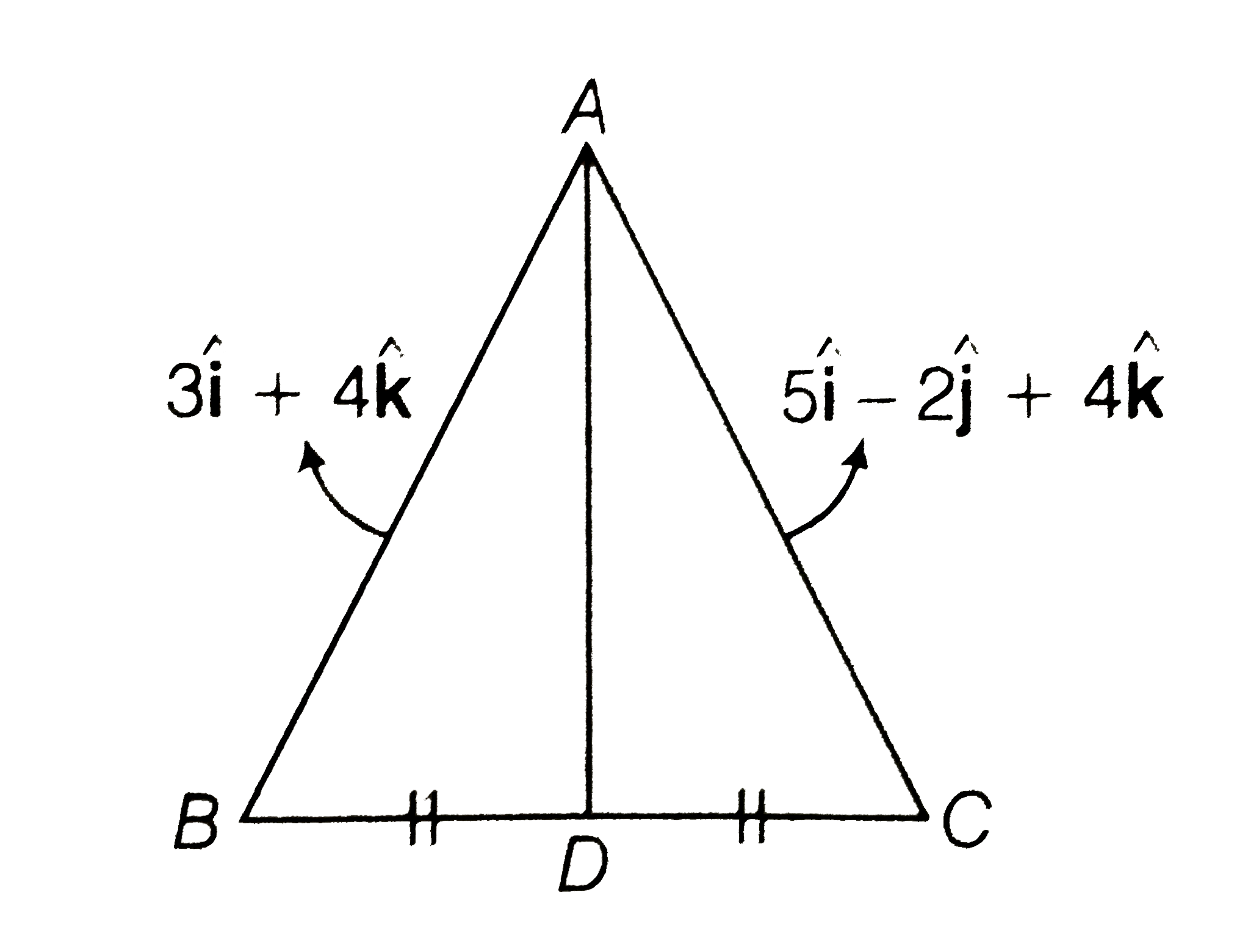
=4ˆi−ˆj+4ˆk
∴|AD|=√(4)2+(−1)2+42
=√16+1+16=√33
Topper's Solved these Questions
Similar Questions
If the vectors −−→AB=3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC, then the length of the median through A is (A) √18 (B) √72 (C) sqrt(33)(D)sqrt(45)
View SolutionThe vectors −−→AB=3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC. The length of the median through A is (A) √72 (B) √33 (C) √2880 (D) √18
View Solution
Knowledge Check
If the vectors AB=3ˆi+4ˆk and AC=5ˆi−2ˆj+4ˆk are the sides of a Δ ABC, then the length of the median through A is
A√18B√72C√33D√288If the vector AB=3ˆi+4ˆk and AC=5ˆi−2ˆj+4ˆk are the sides of a ΔABC then the length of the median through A is
A√18B√72C√33D√288If the vectors AB=3ˆi+4ˆkandAC=(5ˆi−2ˆj+4ˆk) are the sides of a ΔABC, then the length of the median through A is
A√18B√72C√33D√288
The vector −−→AB=3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are sides of a triangle ABC. The length of the median through A is (A) √18 (B) √72 (C) √33 (D) √288
View SolutionThe vector ¯¯¯AB=3ˆi+4ˆk and ove→owAC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC. The length of the median through A is
View SolutionIf the vectors −−→AB=3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC, then the length of the median through A is (A) √33 (B) √45 (C) √18 (D) √720
View SolutionIf the vectors ¯¯¯¯¯¯AB=3ˆi+4ˆk and ¯¯¯¯¯¯AC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC, then the length of the median through A is
View SolutionThe vectors −−→AB=3ˆi+5ˆj+4ˆk and −−→AC=5ˆi−5ˆj+2ˆk are the sides of a triangle ABC. The length of the median through A is :
View Solution
