The phase space diagram for harmonic motion is a circle centered at the origin as shown in figure. The to circles represent the same oscillator but for different initial conditions and E1 and E2 are the total mechanical energy, respectively . Then

E1=√2E2
E1=2E2
E1=4E2
E1=16E2
The correct Answer is:C
Step by step video & image solution for The phase space diagram for harmonic motion is a circle centered at the origin as shown in figure. The to circles represent the same oscillator but for different initial conditions and E_(1) and E_(2) are the total mechanical energy, respectively . Then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two identical blocks 1 and 2, each of mass m, are kept on a smooth horizontal surface, connected to three springs as shown in the figure. Each spring has a force constant k. Under suitable initial conditions, the two blocks oscillate in phase and their respective displacement from the mean position is given by
x1=Asinωt and x2=Asinωt
(i) Suggest one such initial condition that will result in such oscillation.
(ii) Find ω

View SolutionFind the phase difference between two particles executing simple harmonic motion with the same frequency if they are found inn the states shown in the figures at four different points of time.
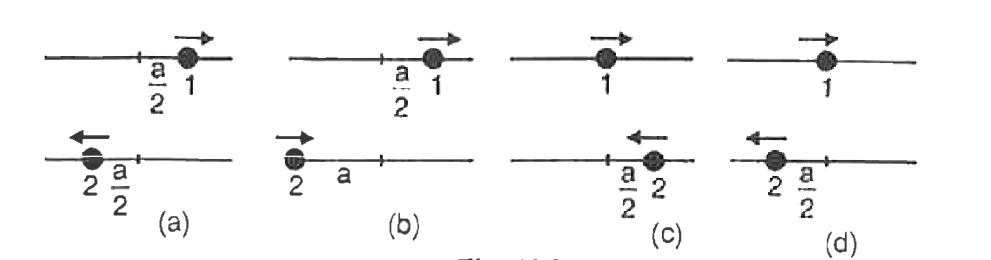
View Solution
Knowledge Check
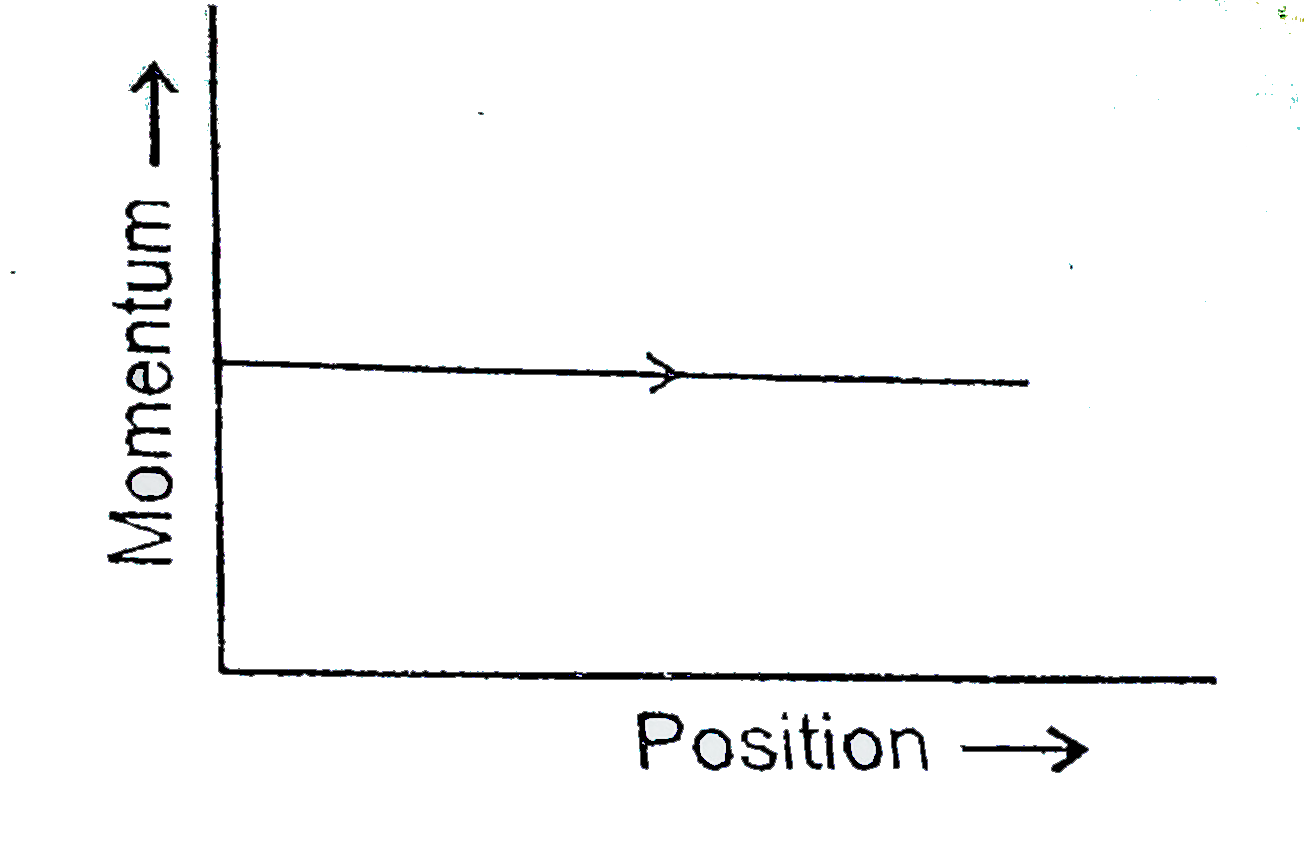
Phase space diagrams are useful tools in analysing all kond of dynamical problems. Theya re especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical system in one-dimelnsion. for such systeam, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. for example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum. upwards (or to right) is positive and downwards (or to left) is negative.
The phase space diagram for simple harmonic motion is a circle cen-tered at the origin.In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 for E2 are the total mechanical energies respectively. Then
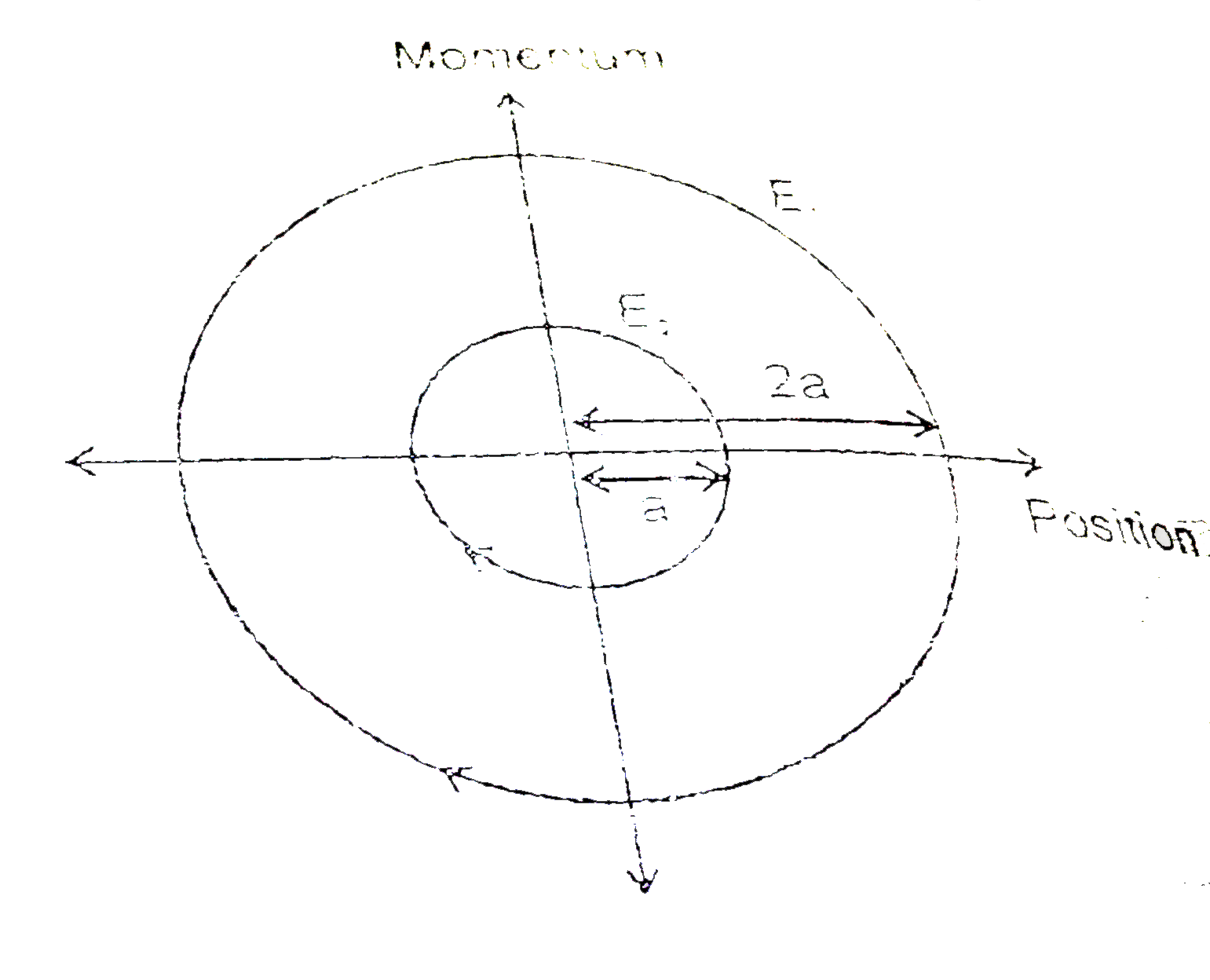 AE1=√2E2BE1=2E2CE1=4E2DE1=16E2
AE1=√2E2BE1=2E2CE1=4E2DE1=16E2Phase space diagrams are useful tools in analysing all kond of dynamical problems. Theya re especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical system in one-dimelnsion. for such systeam, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. for example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum. upwards (or to right) is positive and downwards (or to left) is negative.

The phase space diagram for simple harmonic motion is a circle cen-tered at the origin.In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 for E2 are the total mechanical energies respectively. Then
 AE1=√2E2BE1=2E2CE1=4E2DE1=16E2
AE1=√2E2BE1=2E2CE1=4E2DE1=16E2Phase space diagrams are useful tools in analysing all kond of dynamical problems. Theya re especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical system in one-dimelnsion. for such systeam, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. for example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum. upwards (or to right) is positive and downwards (or to left) is negative.

The phase space diagram for simple harmonic motion is a circle cen-tered at the origin.In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 for E2 are the total mechanical energies respectively. Then
 AE1=√2E2BE1=2E2CE1=4E2DE1=16E2
AE1=√2E2BE1=2E2CE1=4E2DE1=16E2
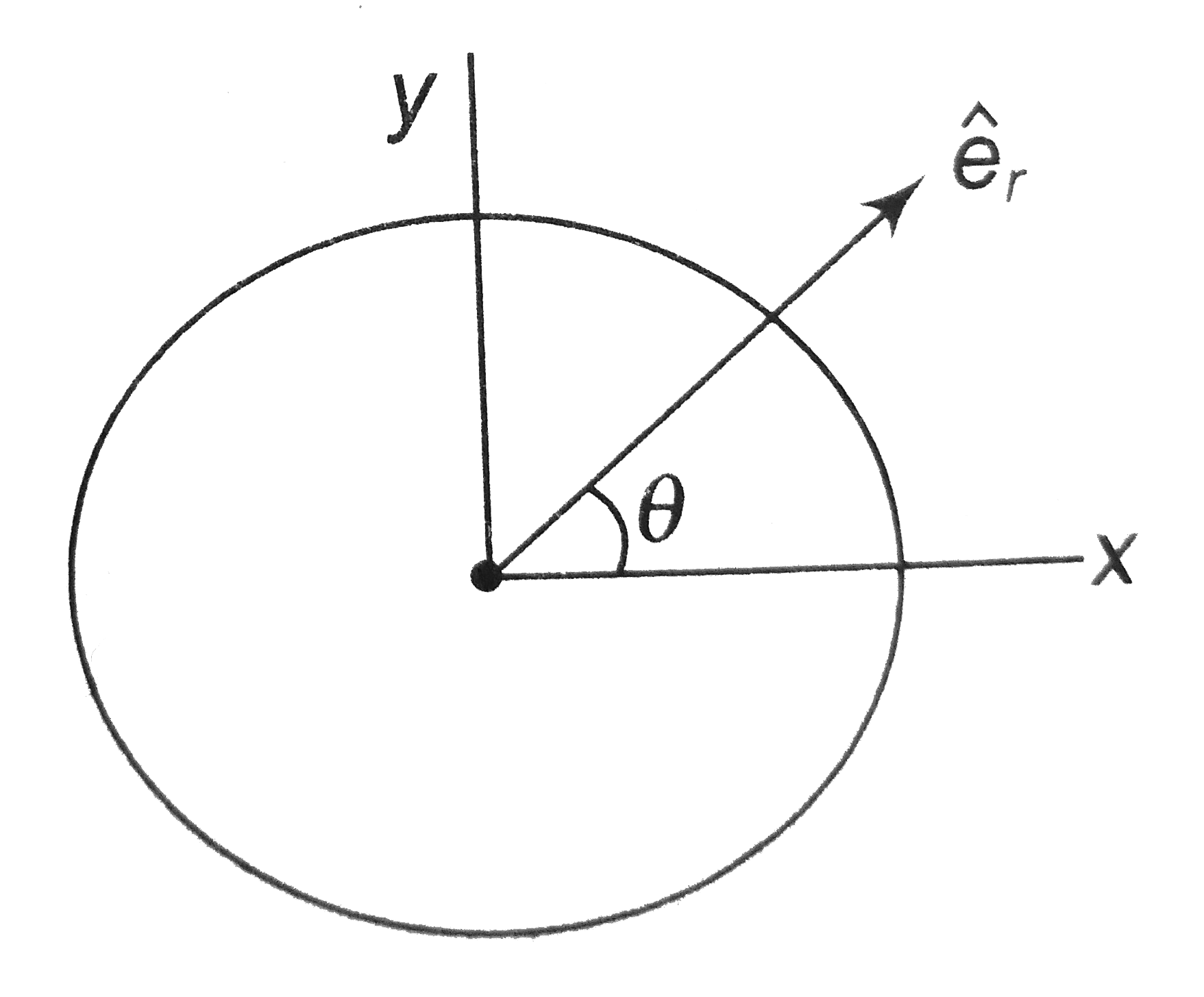
ˆer is unit Vector along radius of a circle shown in figure ˆer can be represented as
View SolutionThe potential energy U(x) of a particle moving along x−axis is shown in figure. Which one of the following graphs represents the variation of kinetic energy of this particel if its total mechanical enery is E0

View SolutionTwo springs of force constants K and 2K are stretched by the same force. If E1 and E2 are the potential energies stored in them respectively then
View SolutionTwo bodies of masses m and 2m have same momentum. Their respective kinetic energies E1 and E2 are in the ratio
View SolutionPhase space diagrams are useful tools in analysing all kond of dynamical problems. Theya re especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical system in one-dimelnsion. for such systeam, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. for example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum. upwards (or to right) is positive and downwards (or to left) is negative.

Consider the spring-mass system, with mass submerged in water, as shown in the figur, the phase diagram for one cycle of this system is :

View Solution
