The equation to the line bisecting the join of (3,-4) and (5,2) and having intercepts on the x-axis and y-axis in the ratio of 2:1 is:

A

x+y-3=0

B

2x-y=9

C

x+2y=2

D

2x+y=7

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let the points be A (3,-4) and B(5,2)
Mid - point of AB = (4,-1)
It is given that the bisecting line intersect the coordinate axes in the ratio 2 :1 .

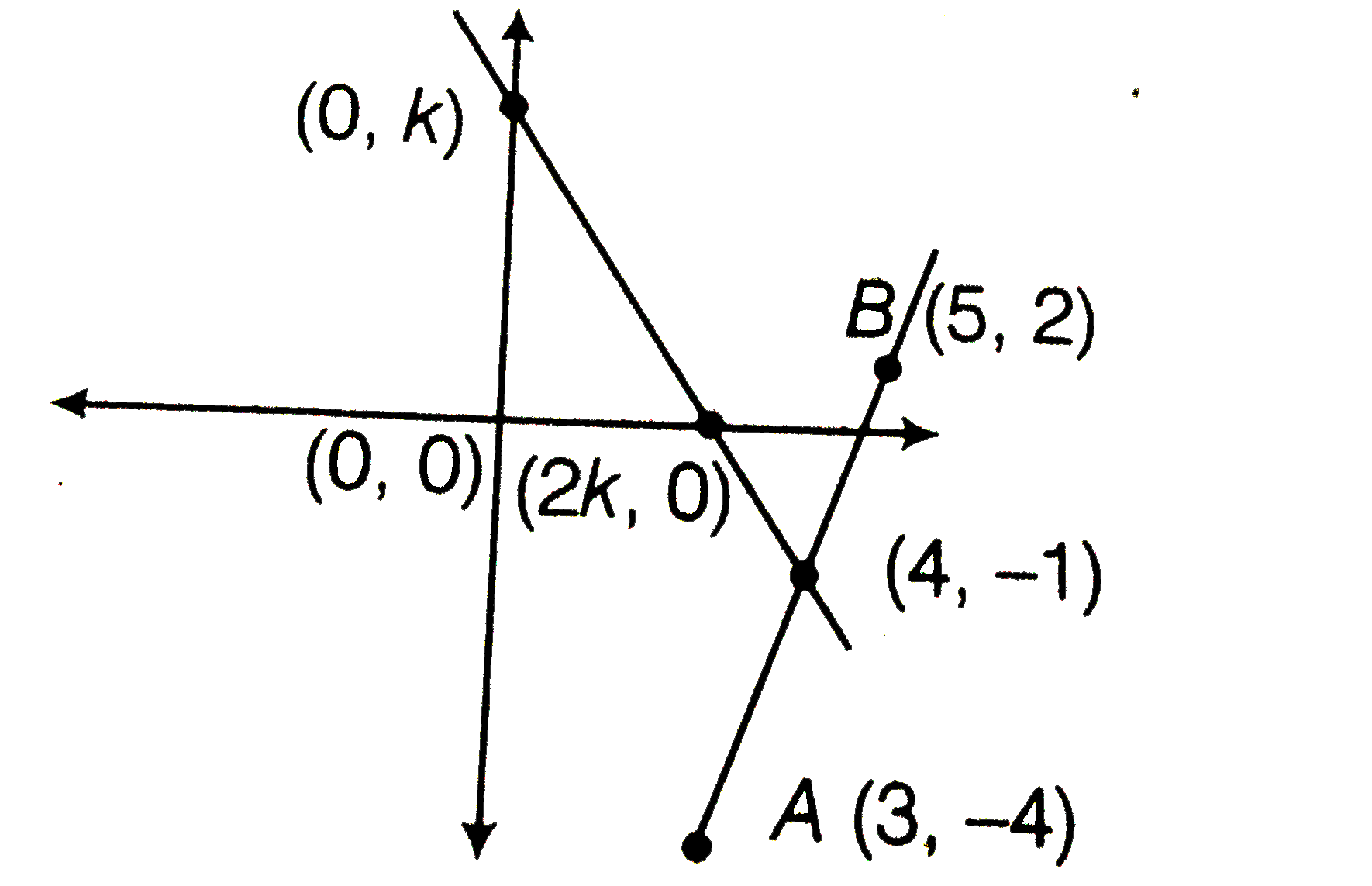
So, point on coordinate axes are (2k, 0) and (0,k) . The equation of line passing through the above point is
$y - 0 = \frac{k - 0}{0 - 2 k} (x - 2 k) \Rightarrow y = - \frac{1}{2} (x - 2 k)$
Since it is passing through the mid-point of AB.i.e. (4,-1)
$- 1 = - \frac{1}{2} (4 - 2 k) \Rightarrow k = 1$
On putting the value of k in Eq. (i) we get ,
$y = - \frac{1}{2} (x - 2) \Rightarrow x + 2 y = 2$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The equation of the line bisecting the join of (3,-4) and (5,2) and having its intercepts on the X-axis and the Y-axis in the ratio $2 : 1$ is
Ax+y-3=0
B2x-y=9
Cx+2y=2
D2x+y=7
Question 2 - Select One
The equation to the line bisecting the joining of (3. - 4) and (5, 2) having its intercepts on X-axis and Y-axis in the ratio 2:1, is
Ax + y - 3= 0
B2x - y = 9
Cx + 2y = 2
D2x + y = 7
Question 3 - Select One
The equation of a line bisecting the join of (2010, 1600) and $(- 1340, 1080)$ and having intercept on the axes in the ratio 1 : 2 is
A $2 x + y = 1680$
B $x + 2 y = 1680$
C $2 x + y = 2010$
Dnone of these

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-STRAIGHT LINE -EXERCISE 2(MISCELLANEOUS PROBLEMS)

Home
Ask Doubt
Profile