Out of 64 students, the number of students taking Mathematics is 45 and number of students taking both Mathematics and Biology is 10. Then, the number of students taking only Biology is
18
19
20
None of these
The correct Answer is:B
Let M and B denote the number of students taking Mathematics and Biology.
Then, n(M)=45,n(M∩B)=10,n(M∪B)=64
n(B)=n(M∪B)−n(M)+n(M∩B)=64−45+10=29
⇒n(B)=n(B)−n(M∩B)=29−10=19
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - Exercise 1 (TOPICAL PROBLEMS) Relation and Equivalence Relation
10 Videos
- SETS, RELATIONS AND FUNCTIONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - Exercise 1 (TOPICAL PROBLEMS) Types of Mapping
10 Videos
- SEQUENCES AND SERIES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEQUENCES AND SERIES EXERCISE - EXERCISE 31
1 Videos
- SOLVED PAPER 2017BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SOLVED PAPER 2017EXERCISE - MCQS
50 Videos
Similar Questions
In a class of 25 students, 12 have taken mathematics, 8 have taken mathematics, but not biology. Find thenumber of students who have taken both mathematics and biology and the number of those who havetaken biology but not mathematics. Each student has taken either mathematics or biology or both.
View SolutionIn a competitive examination, 250 students have registered. Out of these, 50 students have registered for Physics, for Mathematics and 35 students for both Mathematics and Physics. What is the number of students who have registered neither for Physics nor for Mathematics?
View Solution
Knowledge Check
In a class of 35 students , 17 have taken Mathematics , 10 have taken mathematics but not economics if each student has taken either mathematics OR Economics or both , then the number of students who have taken Economics but not mathematics is
A7B25C18D3272% of the students of a certain class took Biology and 44% took Mathematics. If each student took at least one subject from Biology or Mathematics and 40 took both, then the total number of students in the class is
A200B240C250D320An investigator interviewed 100 students to determine the performance of three drinks: milk , coffee and tea the in vestigotor reported that 10 students take all three drinks milk . Coffe and tea , 20 students take take coffe , 25 students take milk only , 5 students take coffee only and 8 students take tea only . then the number of students who did not take any of these drinks is
A10B20C25D30
In a class of 25 students, 12 have taken Mathematics, 8 have taken Mathematics but not Biology. The number of students who have taken both Mathematics and Biology is (a) 4 (b) 8 (c) 24 (d) 36
View SolutionIn Class XI of a certain school, there are 30 students in a Mathematics class and 20 students in Biolog class. Find the number of students which are in Mathematics class or in Biology class in the following cases:
(i) Two classes are conducted at the same time.
(ii) Two classes are condcuted at different time and 5 students study both the subject
View SolutionThe diagram represents the number of students studying different subjects. What is the number of students who study History and Biology?
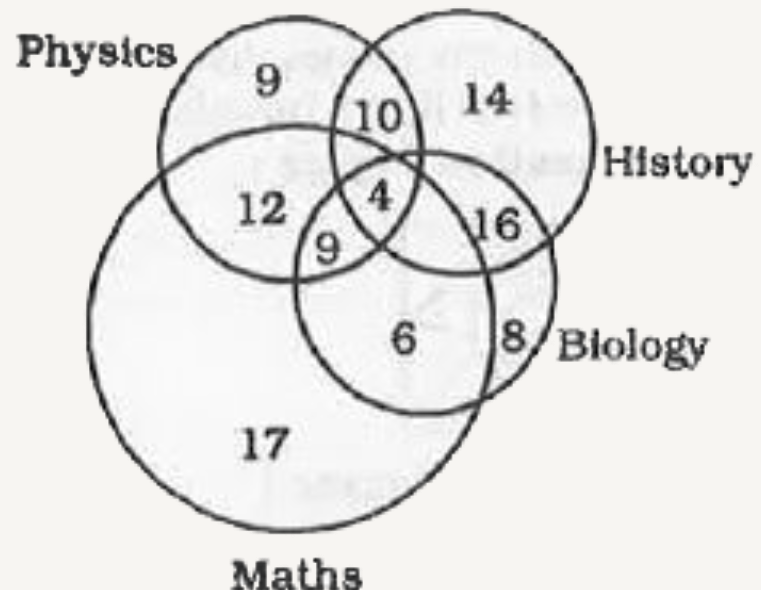
View SolutionIn a class of 100 students, 55 students have passed in Mathematics and 67 students have passed in Physics. Then the number of students who have passed in Physics only is
View SolutionIn a class of 80 students, 55 students passed in mathematics and 60 passed in chemistry. 10 stu-dents failed in both mathematics and chemistry.
(i) How many students passed in both the subjects ?
(ii) How many students passed in exactly one of the two subjects ?
View Solution
