Maximum area of a reactangle which can be inscribed in a circle of a given radius R is

A

$π r^{2}$

B

$r^{2}$

C

$π r^{2} / 4$

D

$2 r^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let length of rectangel is be $2 x$ .
Ara of rectangle $A = 2 x .2 \sqrt{r^{2} - x^{2}} = 5 x \sqrt{r^{2} - x^{2}}$
$\Rightarrow \frac{d A}{d x} = \frac{4 (r^{2} - 2 x^{2})}{\sqrt{r^{2} - x^{2}}}$
For maximum or minimum put
$\frac{d A}{d x} = 0 \Rightarrow x = \frac{r}{\sqrt{2}}$
It can be easily checked that $\frac{d^{2} A}{{d x}^{2}} < 0$
for $x = \frac{r}{\sqrt{2}}$

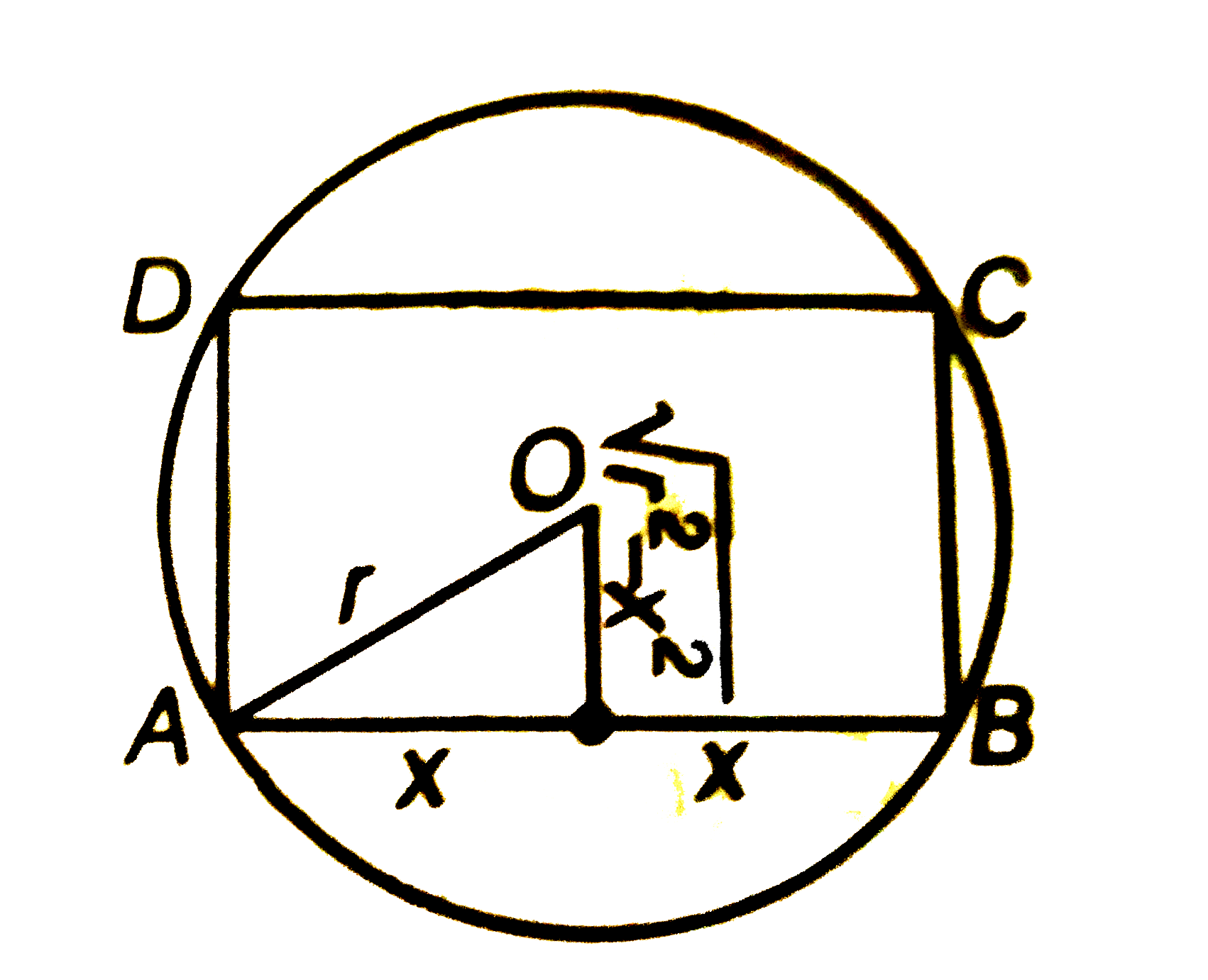
The maximum value of A is given by
$A = 4 \frac{r}{\sqrt{2}} \sqrt{r^{2} - \frac{r^{2}}{2}} = 2 r^{2}$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
What is the maximum area of a triangle that can be inscribed in a circle of radius a?
(a) $\frac{3 a^{2}}{4}$
(b) $a^{2}$
(c) $\frac{3 \sqrt{3} a^{2}}{4}$
(d) $\frac{\sqrt{3} a^{2}}{4}$
A $\frac{3 a^{2}}{4}$
B $\frac{a^{2}}{2}$
C $\frac{3 \sqrt{3} a^{2}}{4}$
D $\frac{\sqrt{3} a^{2}}{4}$
Question 2 - Select One
The area of the largest triangle that can be inscribed in a semicircle of radius r is :
A $r^{2} c m^{2}$
B ${(\frac{r}{3})}^{2} c m^{2}$
C $r \sqrt{2} c m^{2}$
D $3 \sqrt{3 r} c m^{2}$
Question 3 - Select One
The area of the largest triangle that can be inscribed in a semicircle of radius r is :
A $r^{2} c m^{2}$
B ${(\frac{r}{3})}^{2} c m^{2}$
C $r \sqrt{2} c m^{2}$
D $3 \sqrt{3} c m^{2}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DERIVATIVES-MHT CET CORNER

Home
Ask Doubt
Profile