The area bounded by the parabola $y^{2} = 8 x,$ the x-axis and the latusrectum, is

A

$16 / 3$

B

$32 / 3$

C

$8 / 3$

D

$64 / 3$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Equation of latusrectum of the parabola $y^{2} = 8 x$ is x = 2.
Therefore,
Required area $= 2 \int_{0}^{2} \sqrt{8 x} d x = 4 \sqrt{2} {[\frac{x^{3 / 2}}{3 / 2}]}_{0}^{2}$

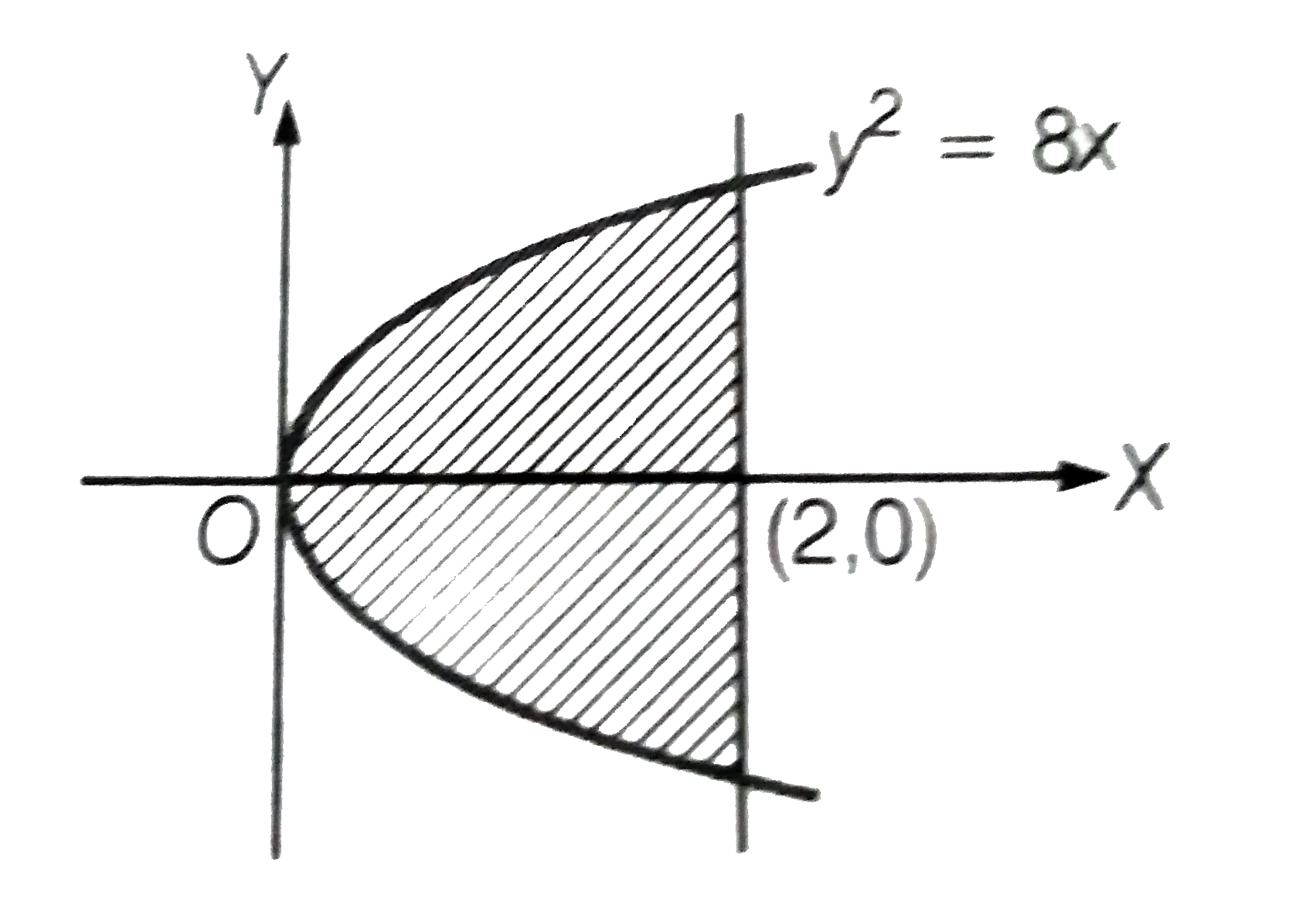
$= 4 \sqrt{2} [\frac{2 \sqrt{2}}{3 / 2}] = \frac{32}{3}$ sq units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Area bounded by the parabola $a y^{2} = x$ , the X-axis and the ordinate at x = a is
A $\frac{2 a^{2}}{3}$
B $\frac{2 a}{3}$
C $\frac{a^{2}}{2}$
D $\frac{3 a^{2}}{2}$
Question 2 - Select One
The area bounded by the parabola $y = x^{2} - 7 x + 10$ and X-axis
A $9 / 2$ sq units
B $1 / 6$ sq units
C $5 / 6$ sq units
DNone of these
Question 3 - Select One
Area of the region bounded by the parabola $a y = x^{2}$ , the X-axis and the ordinates at x = a, x = 2a is
A $\frac{3 a^{2}}{7}$
B $\frac{3 a}{7}$
C $\frac{7 a}{3}$
D $\frac{7 a^{2}}{3}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DEFINITE INTEGRALS -MHT CET Corner

Home
Ask Doubt
Profile