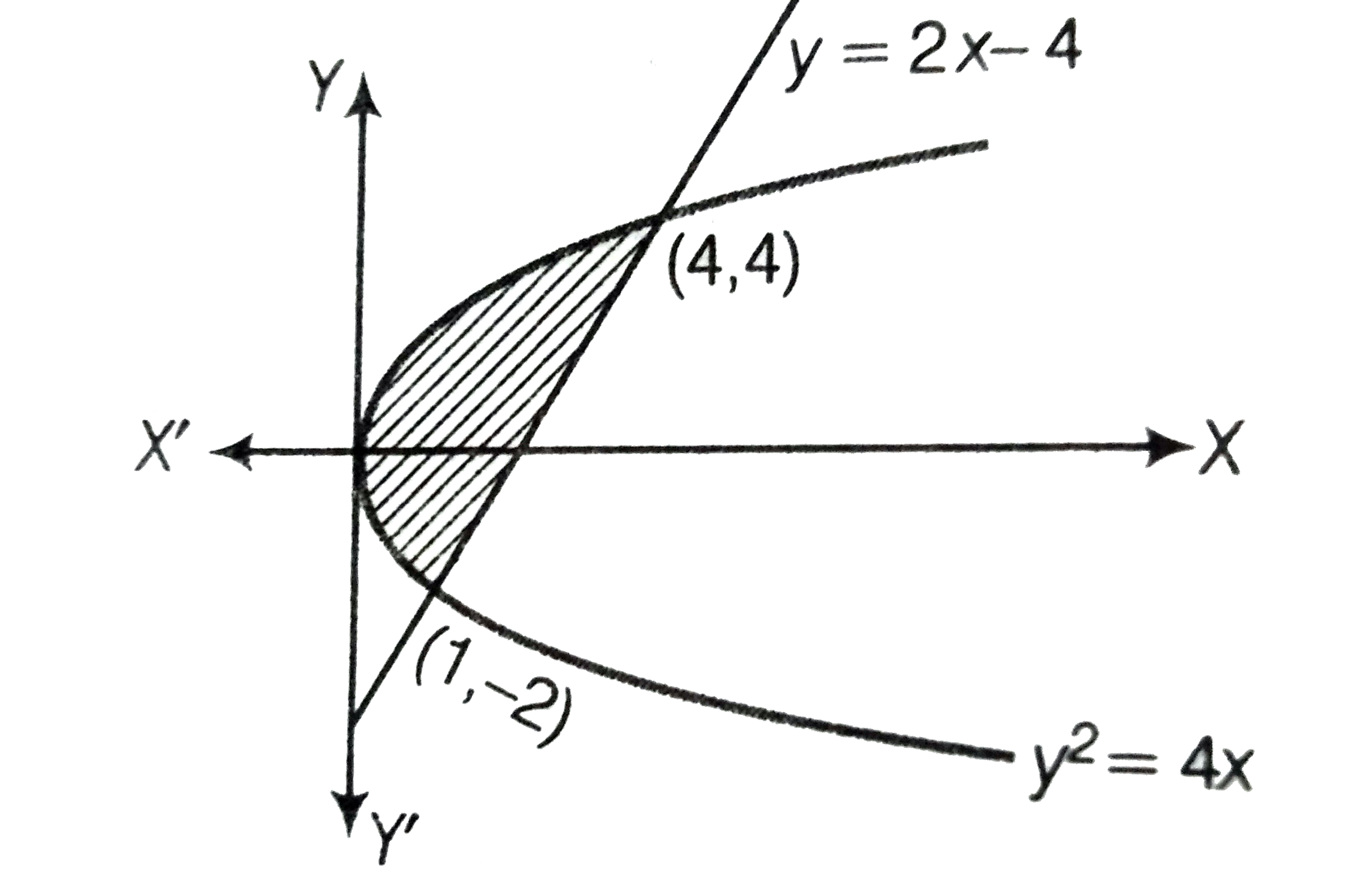
The area bounded between the parabola $y^{2} = 4 x$ and the line y = 2x - 4 is equal to

A

$\frac{17}{3}$ sq units

B

$\frac{19}{3}$ sq units

C

9 sq units

D

15 sq units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

The point of intersection of $y^{2} = 4 x$ and y = 2x - 4 is ${(2 x - 4)}^{2} = 4 x$

$\Rightarrow 4 x^{2} + 16 - 16 x = 4 x$
$\Rightarrow 4 x^{2} - 20 x + 16 = 0$
$\Rightarrow x^{2} - 5 x + 4 = 0$
$\Rightarrow (x - 1) (x - 4) = 0$
$\Rightarrow x = 1, 4 \Rightarrow y = - 2, 4$
$∴$ Required area $= \int_{- 2}^{4} (\frac{y + 4}{2}) d y - \int_{- 2}^{4} \frac{y^{2}}{4} d y$
$= \frac{1}{2} {[\frac{y^{2}}{2} + 4 y]}_{- 2}^{4} - \frac{1}{4} {[\frac{y^{3}}{3}]}_{- 2}^{4}$
$= \frac{1}{2} [8 + 16 - (2 - 8)] - \frac{1}{12} [64 + 8]$
$= 15 - 6 = 9$ sq units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area bounded by the parabola $y^{2} = 4 a x$ and the lines x = a and x = 4a, is
A $\frac{35 a^{2}}{3}$
B $\frac{4 a^{2}}{3}$
C $\frac{7 a^{2}}{3}$
D $\frac{56 a^{2}}{3}$
Question 2 - Select One
The area bounded by the parabola $x^{2} = 2 y$ and the line y=3x is
A4 sq. units
B18 sq. units
C24 sq. units
D32 sq. units
Question 3 - Select One
Area bounded between the curve $x^{2} = y$ and the line y = 4x is
A $\frac{32}{3}$ sq units
B $\frac{1}{3}$ sq unit
C $\frac{8}{3}$ sq units
D $\frac{16}{3}$ sq units

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DEFINITE INTEGRALS -MHT CET Corner

Home
Ask Doubt
Profile