Find the area included between the line $y = x$ and the parabola $x^{2} = 4 y$ .

A

$\frac{8}{3}$ sq units

B

$\frac{4}{3}$ sq units

C

$\frac{9}{4}$ sq units

D

$\frac{7}{3}$ sq units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Equation of parabola is $x^{2} = 4 y$ and equation of line is y = x.
Solving, we get $x^{2} = x$
or $x (x - 4) = 0$
$∴ x = 0, 4$
$∴$ Line y = x cuts parabola at two points O and

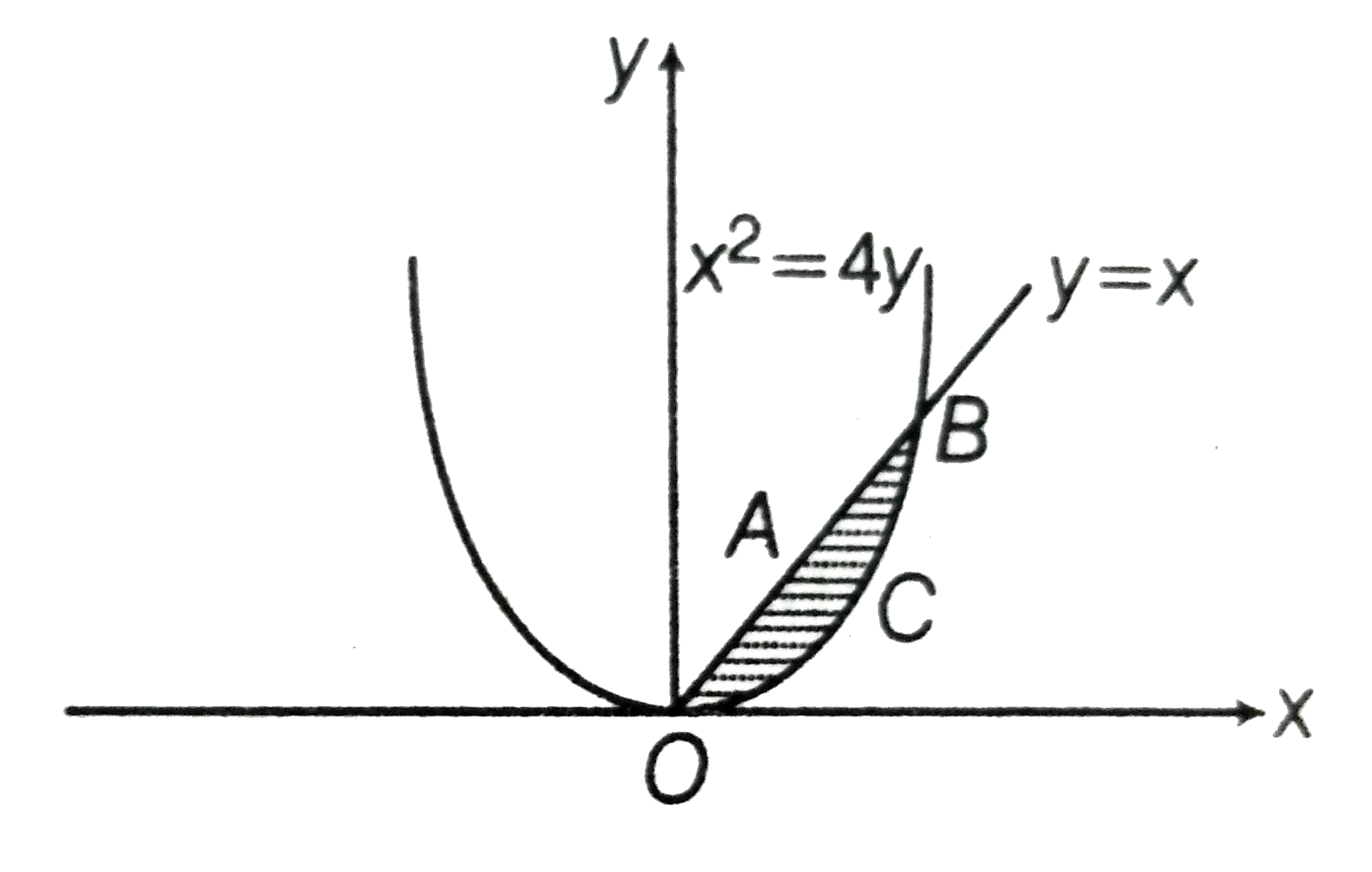
B, x-coordinate of O is 0 and x-coordinate of B is 4.
Required area = area OCBAO
$= \int_{0}^{4} (y_{1} - y_{2}) d x = \int_{0}^{4} (x - \frac{x^{2}}{4}) d x$
$= {[\frac{x^{2}}{2} - \frac{x^{3}}{12}]}_{0}^{4} = [\frac{16}{2} - \frac{64}{12}] = \frac{8}{3}$ sq units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area included between the parabolas $y^{2} = 4 x and x^{2} = 4 y$ is
A $\frac{8}{3} sq. units$
B $8 sq. units$
C $\frac{16}{3} sq. units$
D $12 sq. units$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DEFINITE INTEGRALS -MHT CET Corner

Home
Ask Doubt
Profile