O(0,0), A(1,2), B(3,4) are the vertices of $Δ O A B$ . The joint equation of the altitude and median drawn from O is

A

$x^{2} + 7 x y - y^{2} = 0$

B

$x^{2} + 7 x y + y^{2} = 0$

C

$3 x^{2} - x y - 2 y^{2} = 0$

D

$3 x^{2} + x y - 2 y^{2} = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

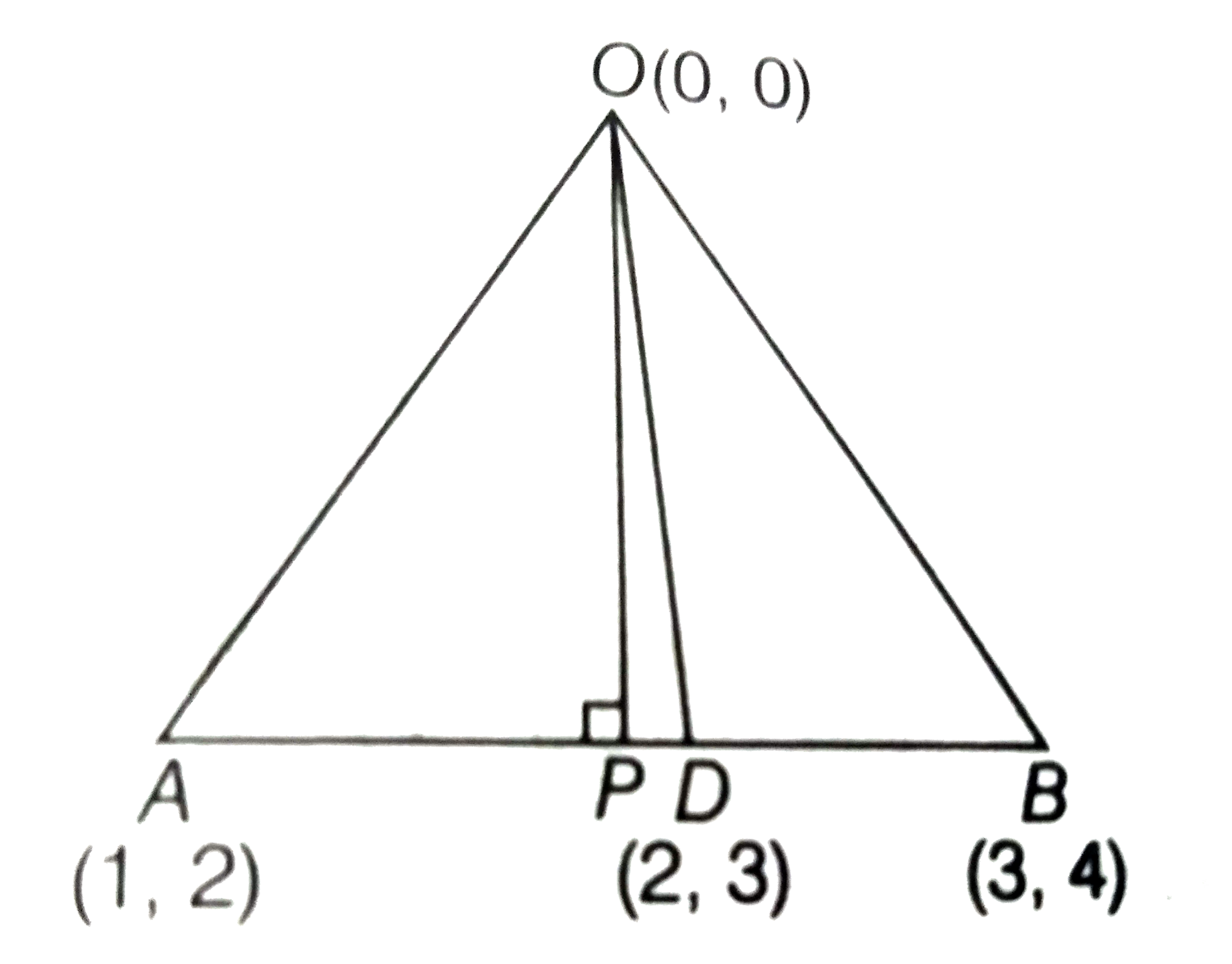
Given, O(0,0), A(1,2) and B(3,4) be the vertices of $Δ O A B$ . Let OP and OD be the altitude and median off $Δ O A B$ , respectively.
$∴$ Coordinates of $D =$ Mid of $A B = (\frac{1 + 3}{2}, \frac{2 + 4}{2})$
$= (\frac{4}{2}, \frac{6}{2}) = (2, 3)$
Now, equation of OD is $(y - 0) = (\frac{3 - 0}{2 - 0}) (x - 0)$
$[∵ y - y_{1} = (\frac{y_{2} - y_{1}}{I} (x_{2} - x_{1}) (x - x_{1}))]$
$\Rightarrow y = \frac{3}{2} ξ m p l i e s 2 y = 3 ξ m p l i e s 3 x - 2 y = 0$
Slope of $O P = \frac{- 1}{Slope of AB}$ [ $∵ P O ⊥ A B$ ]
$= \frac{- 1}{(\frac{3 - 1}{4 - 2})} = \frac{- 1}{\frac{2}{2}} = - 1$
$∴$ Equation of OP is (y-0)=-1(x-0)
$[∵ y - y_{1} = slope (x - x_{1})]$
$\Rightarrow y = - x$
$\Rightarrow x + y = 0$
Now, joint equationn of OP and OD
$(x + y) (3 x - 2 y) = 0$
$3 x^{2} - 2 x y + 3 x y - 2 y^{2} = 0$
$\Rightarrow 3 x^{2} + x y - 2 y^{2} = 0$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If A (1,-2), B (-2,3) and C(2,-5) are the vertices of $Δ$ ABC, then the equation of the median BE is
A7x+13y+47=0
B13x+7y+5=0
C7x-13y+5=0
Dnone of these
Question 2 - Select One
The joint equation of the lines $3 x + 2 y - 1 = 0 and x + 3 y - 2 = 0$ is
A $3 x^{2} + 11 x y + 6 y^{2} - 7 x + 7 y + 2 = 0$
B $3 x^{2} + 11 x y + 6 y^{2} + 7 x - 7 y + 2 = 0$
C $3 x^{2} + 11 x y + 6 y^{2} - 7 x - 7 y + 2 = 0$
D $3 x^{2} + 11 x y + 6 y^{2} + 7 x + 7 y + 2 = 0$
Question 3 - Select One
The joint equation of the lines $x + 2 y - 1 = 0 and 2 x - 3 y + 2 = 0$ is
A $2 x^{2} + x y - 6 y^{2} + 7 y - 2 = 0$
B $2 x^{2} - x y - 6 y^{2} + 7 y - 2 = 0$
C $2 x^{2} + x y + 6 y^{2} + 4 y - 2 = 0$
D $2 x^{2} - x y + 6 y^{2} - 4 y - 2 = 0$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-SOLVED PAPER 2017-MCQS

Home
Ask Doubt
Profile