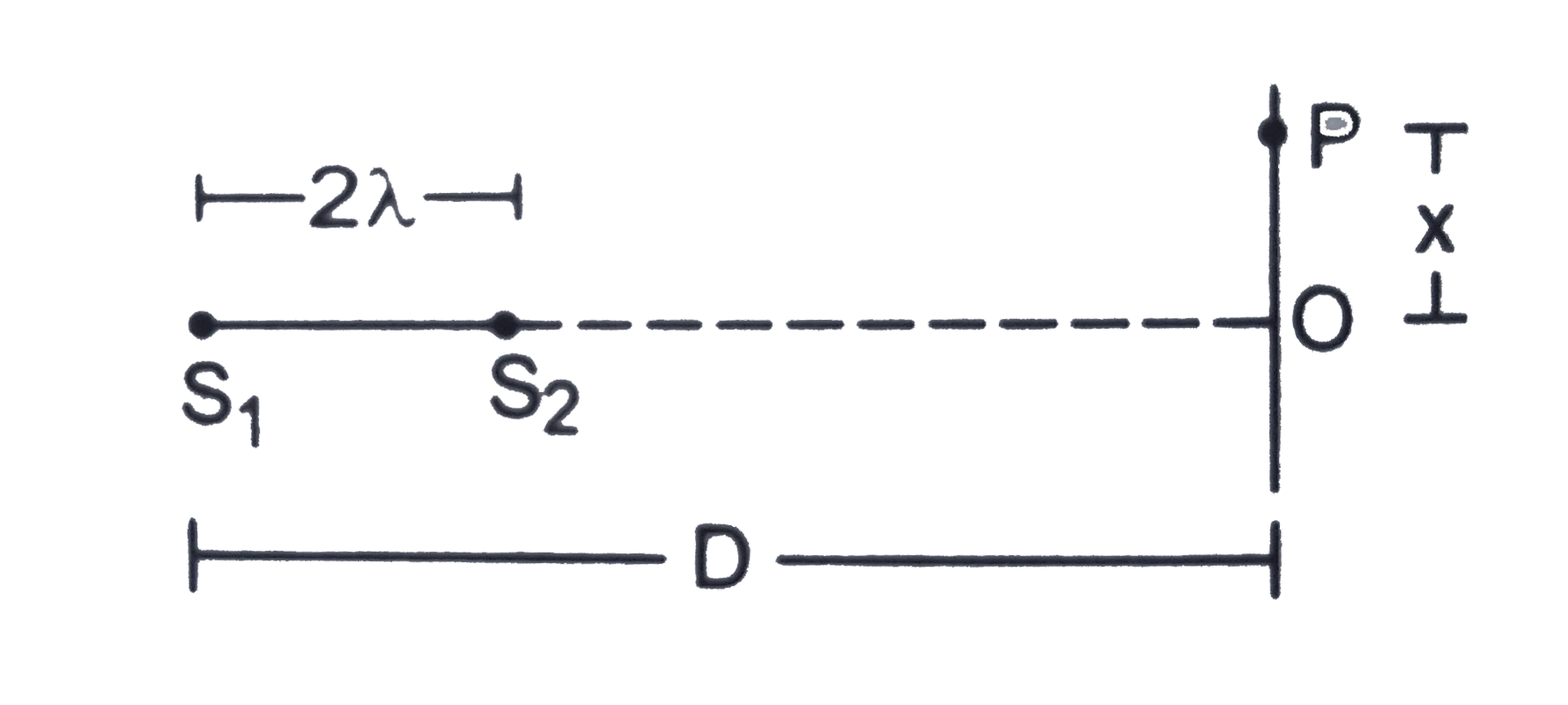
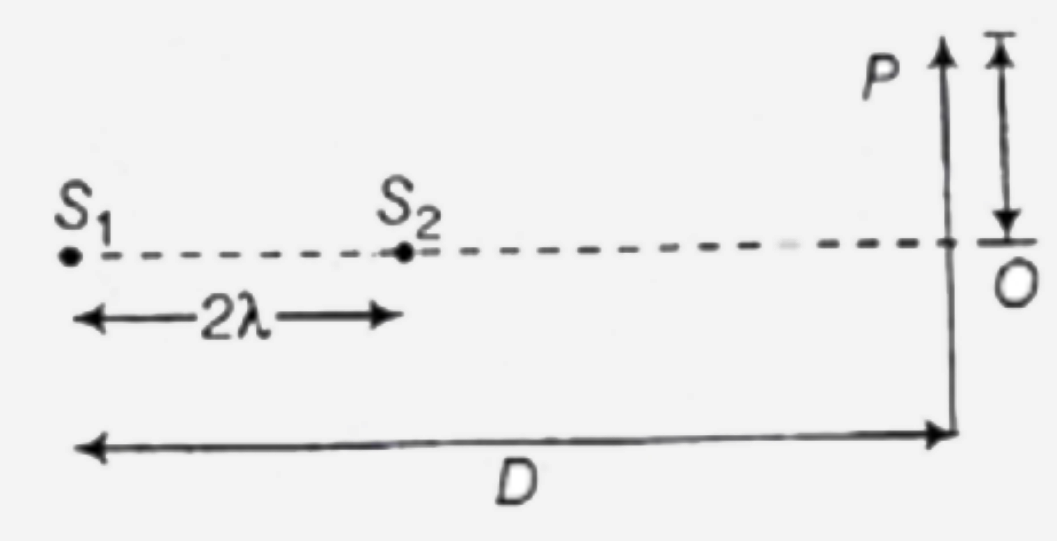
Two coherent narrow slits emitting sound of wavelength lamda in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(gtgtlamda) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.
The correct Answer is:C, D
Since S1,S2 are in same phase at O there wil be maximum intensity.
Given that there will be a maximum intensity at P.
→pathd⇔erence=△x=nl
From the ure (in question)
(S1P)2−(S2P)2
=(sqrtD^2+x_2)^2-[(sqrtD-2lamda^2+x^2]^2<br>=4lamdaD=4lamda^2=4lamdaD<br>(lamda^2issosmallandcan²cted)<br>S_1P-S_2P=(4lamdaD)/(2sqrt(x^2+D^2))=nlamda<br>=(2D)/(sqrt(x^2+D^2))=n<br>rarr n^2(x^2+D^2)=4D^2<br>rarr x=D/n sqrt4-n^2<br>Whenn=1, x=sqrt3D(1st order)<br>n=2,<br>x=0 (2nd order)
∴Wenx=√3D
at P there will be maximum intensity
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Objective -25videos
SOUND WAVES
- BOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises32videos
SOME MECHANICAL PROPERTIES OF MATTER
- BOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Exercises35videos
SPECIFIC HEAT CAPACITIES OF GASES
Similar Questions
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallet to each other at a small separation of 2λ . The sound is delected by maving a delector on the screen at a distance D(>>λ) from the slit S1 as shows in figure. Find the distance y such that the intensity at P is equal to intensity at O .
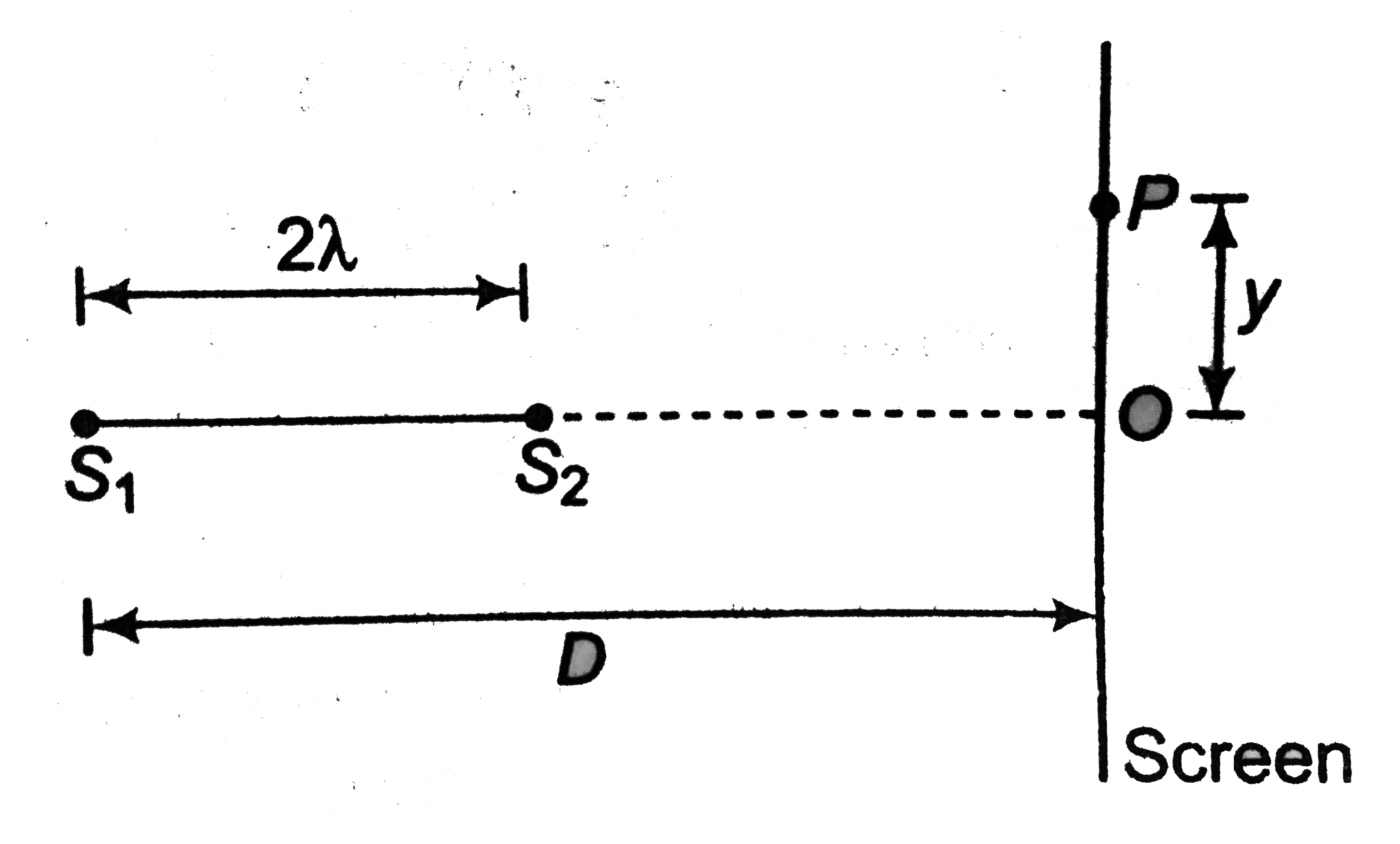
View SolutionTwo coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallet to each other at a small separation of 2λ . The sound is delected by maving a delector on the screen at a distance D(>>λ) from the slit S1 as shows in figure. Find the distance y such that the intensity at P is equal to intensity at O .
View Solution
Knowledge Check
- Question 1 - Select One
_E01_037_Q01.png)
Two coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 3λ the light is collected on a screen S which is placed at a distance D(>>λ) from the slits the smallest distance x such that the P is a maxima.A√3DB√8DC√5DD√5D2 - Question 2 - Select One
Choose the most appropriate option.
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ. The light is collected ona screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to intensity at O.
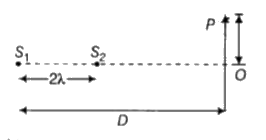A√2DB√3DC√8DD√5D
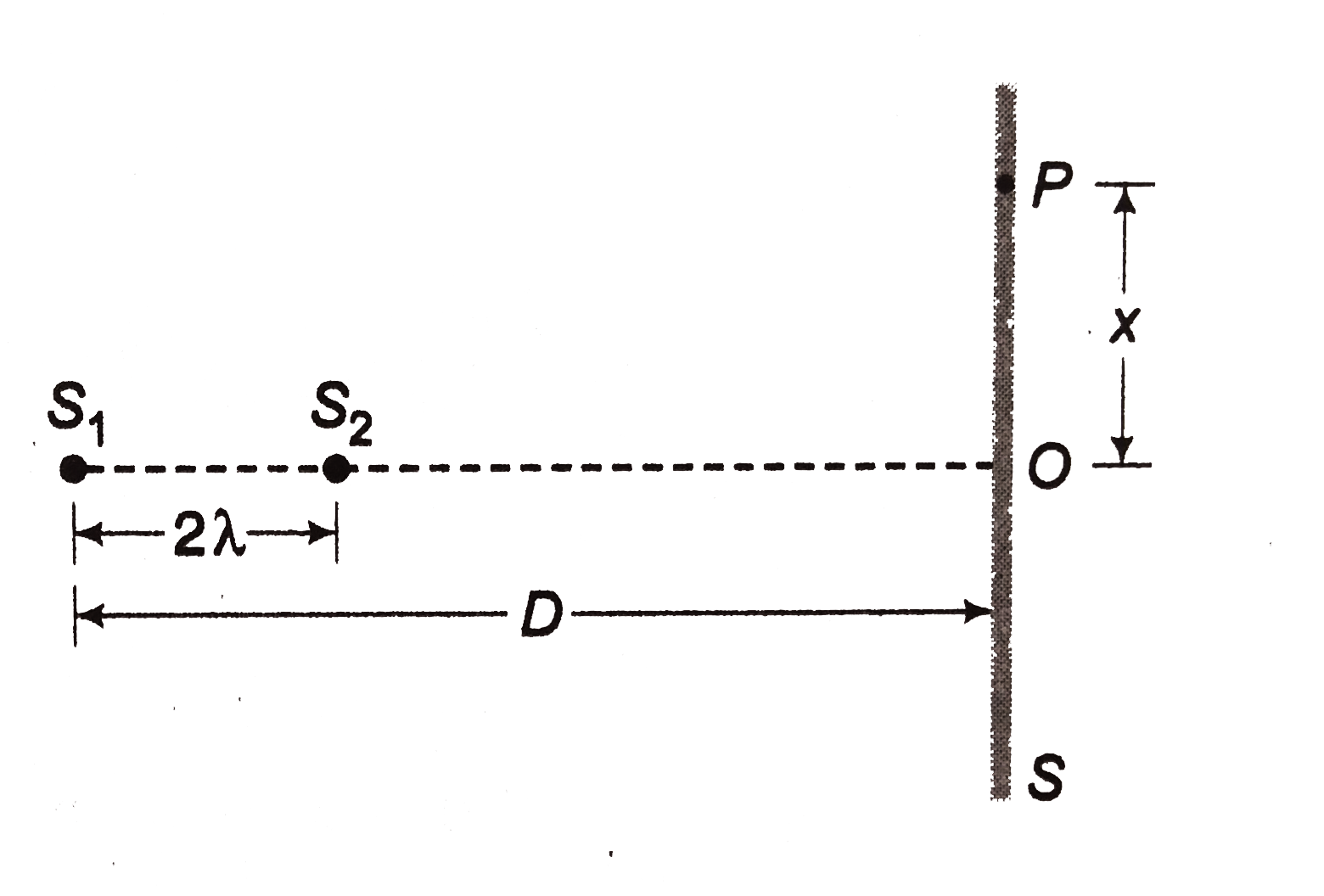
Two coherent narrow slits emitting wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ, the sound is detected by moving a detector on the screen S at a distance D(>>λ) from the slit S1 as shown in Fig. 7.76. Find the distance x such that the intensity at P is equal to the intensity at O.
View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
.View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
.View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
View SolutionA narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror as shown in figure. The light coming directly from the slit and that coming after the reflection interference at a screen ∑ placed at a distance LD from the slit. a. What will be the intensity at a point just above the mirror. i.e., just above O? b. At what distance from O does the first maximum occur?
?
View SolutionA narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror as shown in figure. The light coming directly from the slit and that coming after the reflection interference at a screen ∑ placed at a distance LD from the slit. a. What will be the intensity at a point just above the mirror. i.e., just above O? b. At what distance from O does the first maximum occur?
?View Solution