A resistance thermometer reads R=20.0Ω,27.5Ω,and50.0Ω at the point (0C), the steam point (100C) and the zinc point (420C) respectively.Assuming that the resistance varies with temperature as RΘ=(1+αΘ+βΘ2) , find the values of R0, alpha and beta. Here Theta represents the temperature on Celsius scale.
Raticep∮(R0)=20Ω
R at steam point (R100)=27.5Ω
Ratz∈cp∮(R420)=50Ω
Rθ=R0(1+αθ+βθ2)
⇒R100=R0+R0αθ+R0βθ2
⇒R100−R0R0=αθ+βθ2
⇒27.5−2020=αθ+βθ2
⇒7.520=α100+β10000........(i)
Again R420=R0(1+αθ+βθ2)
⇒50−R020=αθ+βθ2
50−2020=420α+176400β
⇒32=420α+176400β.............(ii)
After solving (i) and (ii), we get
α=3.8×10−3^0C,
β=−5.6×10−7^0C
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Exercises
39 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE
1 Videos
Similar Questions
A platinum resistancethermometer reads 00at the ice point and boiling point of water respectively. The resistance of a platnum wire varies with Celsius temperature θ as Rt=R0(1+αθ+βθ2), where α=3.8×10−3^0C−1 and β=−5.6×10−7^0C−2. What will be the reading of this thermometer if it is pleaced in a liquid bath maintained at 500C?
View SolutionThe resistances of a platinum resistane thermometer are 2.5Ω,4.0Ω, and 7.3Ω at 0∘C,100∘C at t∘C respectively. Calculate t.
View Solution
Knowledge Check
Resistance of a resistor at temperature t∘CisRt=R0(1+αt+βt2), where R0 is the resistance at 0∘C. The temperature coefficient of resistance at temperature t∘C is
A(1+αt+βt2)α+2βtB(α+2βt)Cα+2βt(1+αt+βt2)Dα+2βt2(1+alpaht+βr2)The resistance of a wire is 5Ω at 50∘C and 6Ω at 100∘C . The resistance of the wire at 0∘C will be
A3ΩB2ΩC1ΩD4ΩThe resistance of a resistance thermometer has values 2.70Ω and 3.70Ω at 0∘C and 100∘C respectively. The temperature at which the resistance is 3.10Ω is
A30∘CB40∘CC60∘CD70∘C
Resistance of a resistor at temperature t∘C is Rf=R0(1+αt+βt2) . Here R0 is the resistance at 0∘C .The temperature coefficient of resistance at temperature t∘C is
View SolutionA platinum resistance thermometer reads 00 when its resistance ia 80Ωand1000 when its resistance is 90Ω. Find the platinum scale at which the resistance ia 86 Omega.
View SolutionThe resistance of a conductor is 5Ω at 50∘C and 6Ω at 100∘C. The resistance at 0∘C is
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is
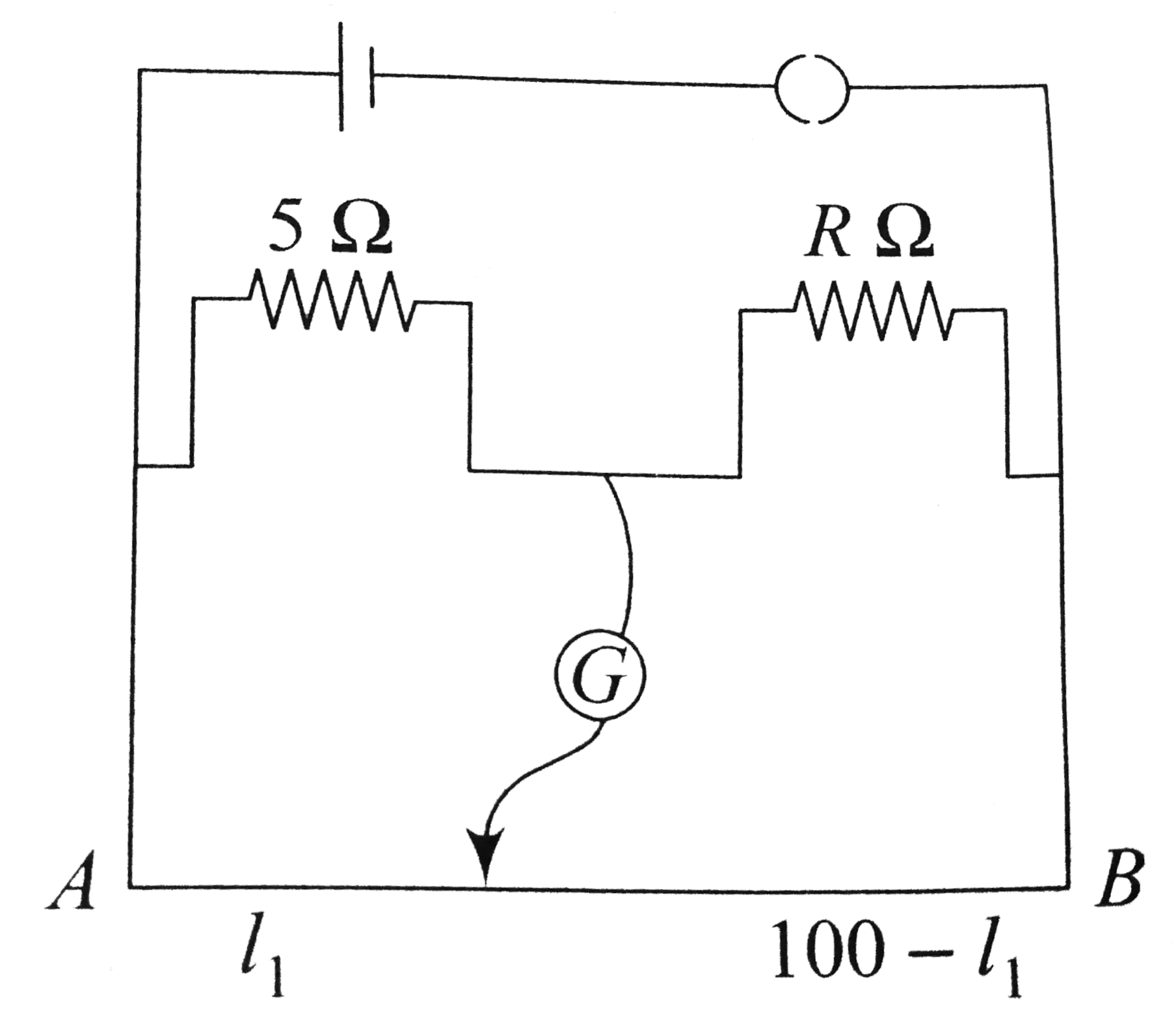
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is

View Solution
