The value of (Cp−Cv) is 1.00R for a gas sample in state A and is 1.08 R in state B. Let (pA,pB)denote the pressures and (TAandTB) denote the temperatures of the states A and B respectively . Most likely
pA<pB and TA>TB
pA>pBandTA<TB
pA=pBandTA<TB
pA>pBandTA=TB
The correct Answer is:A
Step by step video, text & image solution for The value of (C_p - C_v) is 1.00 R for a gas sample in state A and is 1.08 R in state B. Let (p_A, p_B)denote the pressures and (T_A and T_B) denote the temperatures of the states A and B respectively . Most likely by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Objective 2
7 Videos
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Exercises
35 Videos
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Short Answer
10 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
- THE FORCESBOOK - HC VERMACHAPTER - THE FORCESEXERCISE - Exercises
12 Videos
Similar Questions
Knowledge Check
The value of Cp−Cv is 1.09R for a gas sample in state A and is 1.00R in state B. Let AA,TB denote the temperature and pA and PB denote the pressure of the states A and B respectively. Then
ApA<pB and TA>TBBpA>pB and TA>TBCpA=pB and TA<TBDpA>pB and TA<TBThe value of CP−Cv=1.00R for a gas in state A and CP−Cv=1.06R in another state. If PA and PB denote the pressure and TA and TB denote the temperature in the two states, then
APA=PB,TA>TBBPA<PB,TA=TBCPA<PB,TA>TBDPA=PB,TA<TBFigure illustrates a cycle conducted with n moles of an ideal gas. In the states a and b the gas temperatures are Ta and Tb respectively. Temperature of the gas in the state C is ltbr)
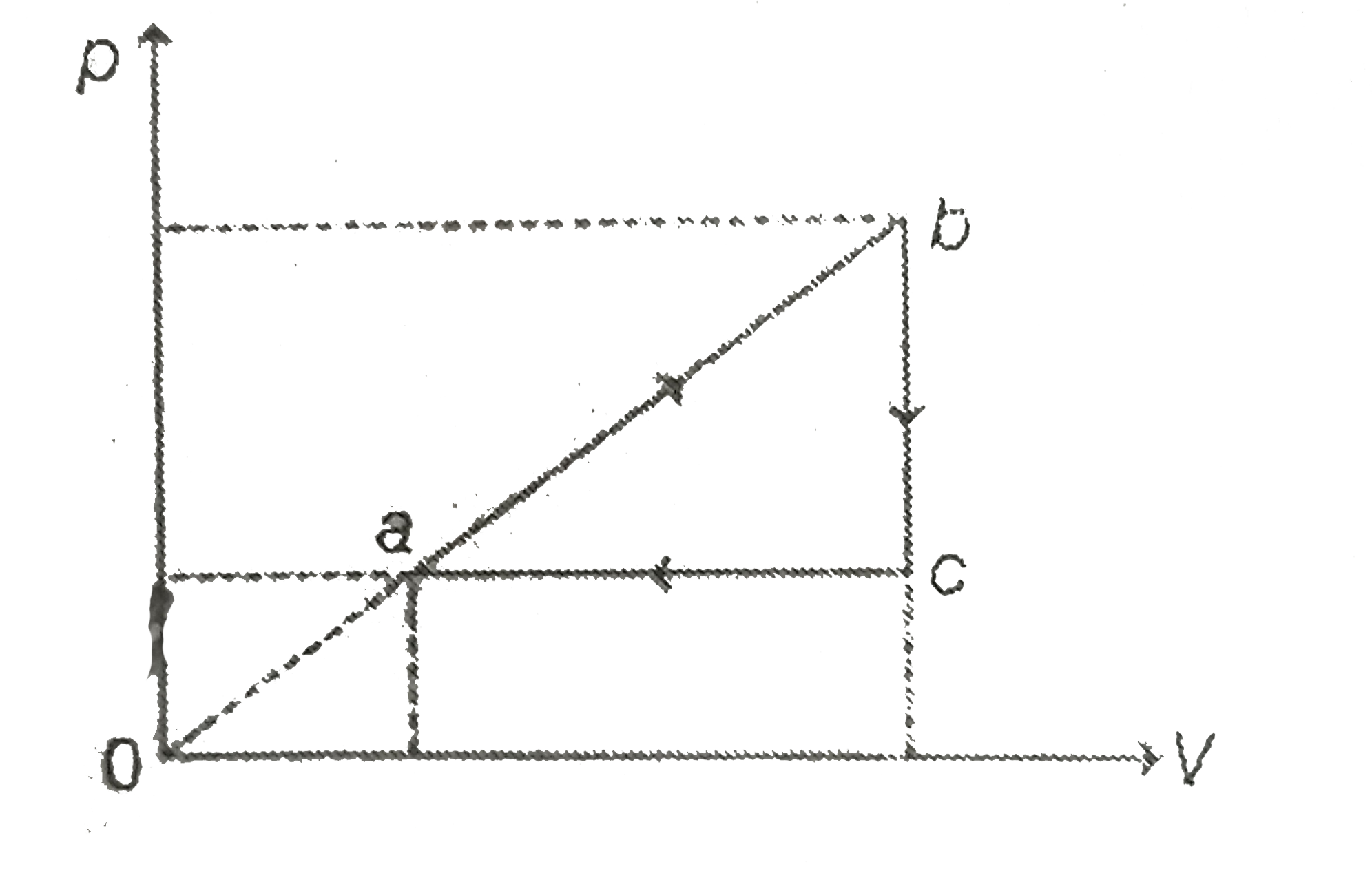 A√TaTbBTa+TbCTaTbTa+TbD(Ta+Tb)/2
A√TaTbBTa+TbCTaTbTa+TbD(Ta+Tb)/2
One mole of monatomic gas is brought from state A to state B. The initial temperature at A is T0. The temperature at B will be –

View SolutionTwo different ideal diatomic gases A and B are initially in the same state. A and B are then expanded to same final volume through adiabatic and isothermal process respectively. If PA,PB and TA,TB represents the final pressure and temperature of A and B respectively then.
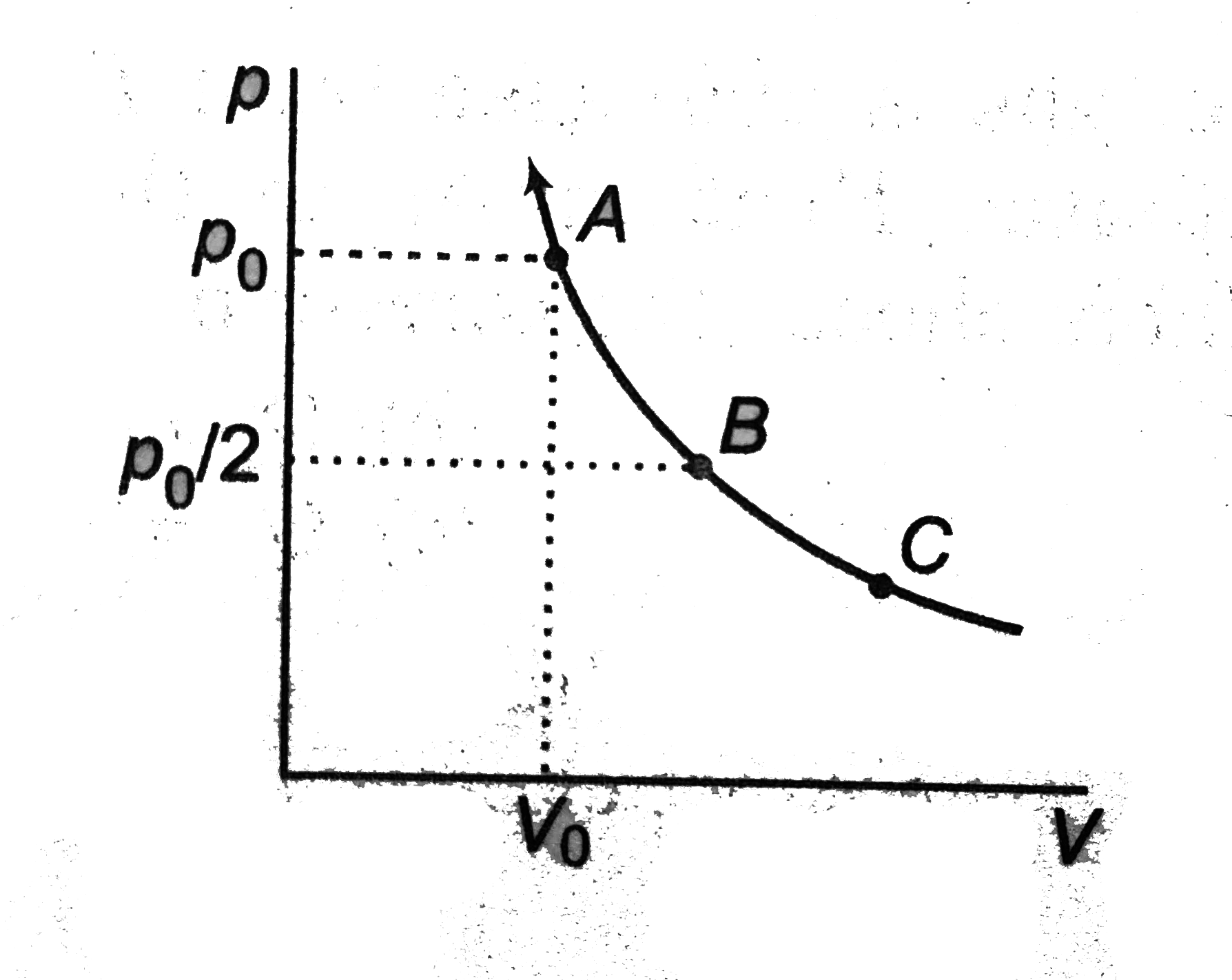
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is
View SolutionThe van der Waal's equation of state for some gases can be expressed as :
(P+aV2)(V−b)=RT
Where P is the pressure , V is the molar volume , and T is the absolute temperature of the given sample of gas and a,b,andR are constants.
The dimensions of constant b are
View SolutionTwo samples A and B are initaially kept in the same state. The sample A is expanded through an adiabatic process and the sample B through an isothermal process. The final volumes of the samples are the same . The final pressures in A and B are pAandPB respectively.
View Solution