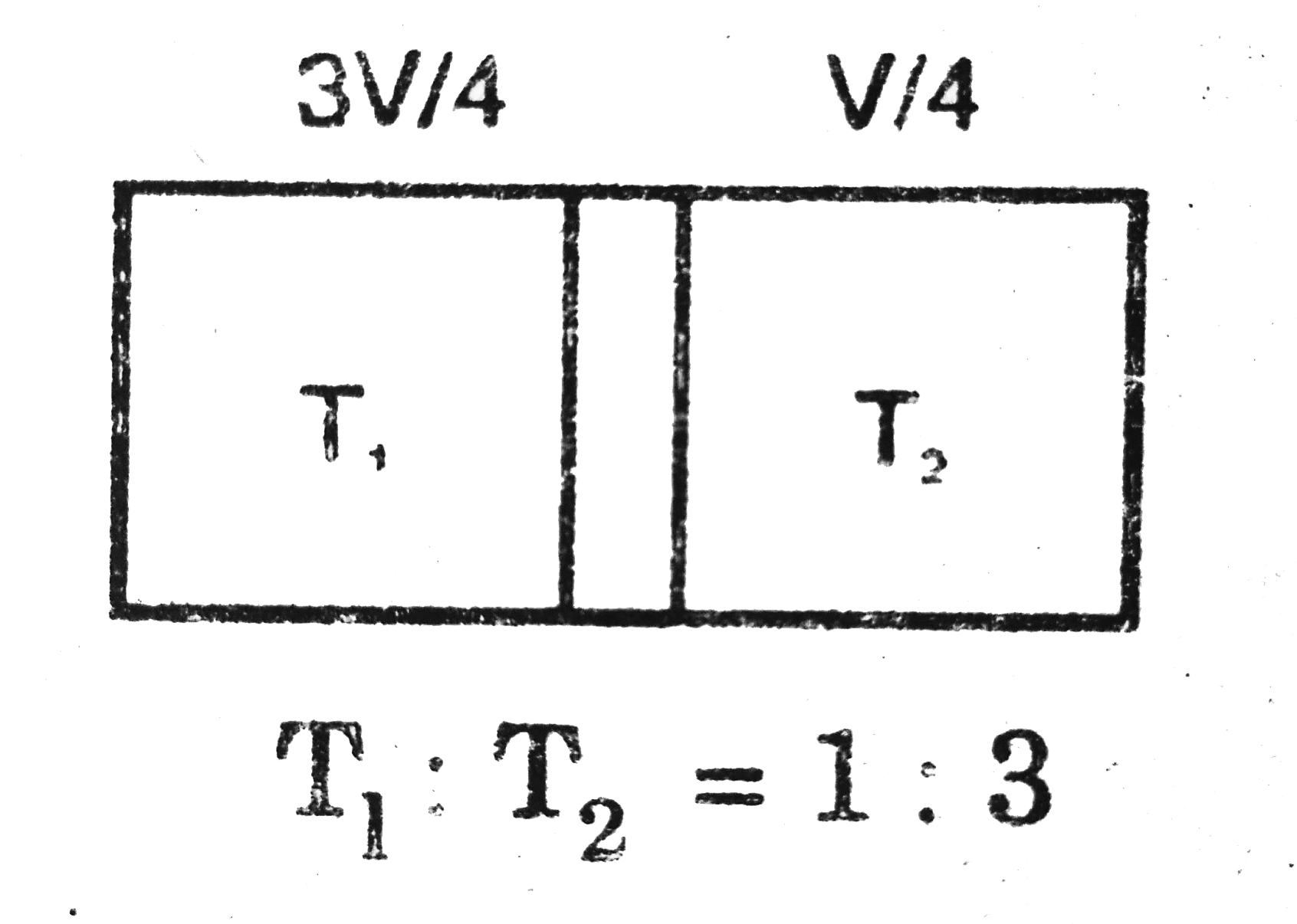
Figure shows a cylindridcal tube with a adibatic walls and fitted with an adiabatic separtor. The separator can be slid into the tube by an external mechanism. An ideal gas(γ=1.5) is injected in the two sides at equal pressures and temperatures . The separator remains in equilibrium at the middel. It is now slid to a position where it divides the tube in the ratio 1:3 Find the ratio of the tempertures in the two parts of the vessel.

Given γ=1.5
We know for adiabatic process TVγ−1
=constant
So, T1Vγ−11=T2Vγ−12 …(equation)
As, it is an adiabatic process and all the other conditions are same, hence the above equation can be applied.
So, T1×(3v4)=T2×(v4)
So, T1:T2=1:3
Topper's Solved these Questions
Similar Questions
Shows a cylindrical tube with adiabatic walls and fittled with a diathermic separetor. The separetor can be slid in the tube by and external mechanism. An ideal gas is injected into the two sides at equal pressures and equal temperatures. The separetor remaons in equilibrium at the middle. It is mow slid to pisition where it devides the tube in the ratio of 1:3. Find the ratio of the pressures in the two parts of the vessel.

View SolutionAn adiabatic cylindrical tube is fitted with an adiabatic separator as shown in figure. Initial separator is in equilibrium and divides a tube in two equal parts. The seperator can be slide into the tube by an extermal mechanism. An ideal gas (γ=1.5) is injected in the two slides at equal pressure and temperature. Now separator is slid to a piston where it divides the tube in the ratio 7:3 The ratio of the temperature in the two parts of the vessel is √n:√7 find n.
View Solution
Knowledge Check
The pressure of gas in cathode ray tube is
A10−2mmB10−3mm of mercuryC105N/m2D1 mm of mercuryFollowing figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P and temperature T in left part and gas at pressure P and temperature T in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)
 AP2BP1CP1(V02)λ(V02+Ax)λDP2(V02)λ(V02+Ax)λ
AP2BP1CP1(V02)λ(V02+Ax)λDP2(V02)λ(V02+Ax)λWhen two capillary tubes A and B are immersed in water , the heights of water columns are found to be in the ratio 2:3 the ratio of the radii of tubes A and B is
A2:3B4:9C9:4D3:2
The trachea divides into two tubes at its lower end. What is the name of these tubes ?
View SolutionFigure shows an adiabatic cylindrical tube of volume (V0) divided in two parts by a frictionless adibatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (p1) and the temperatures (T1) is injected into the left part and the another ideal gas at pressures (P2) and temperature (T2) is injected into the right part. (CpCv=γ) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the parts, (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.

View SolutionIn given figure, an adiabatic cylindrical tube of volume 2V0 is divided in two equal parts by a frictionless adiabatic separator. An ideal gas in left side of a tube having pressure P1 and temperature T1 where as in the right side having pressure P2 and temperature T2.Cp/Cv=γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the final volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases,
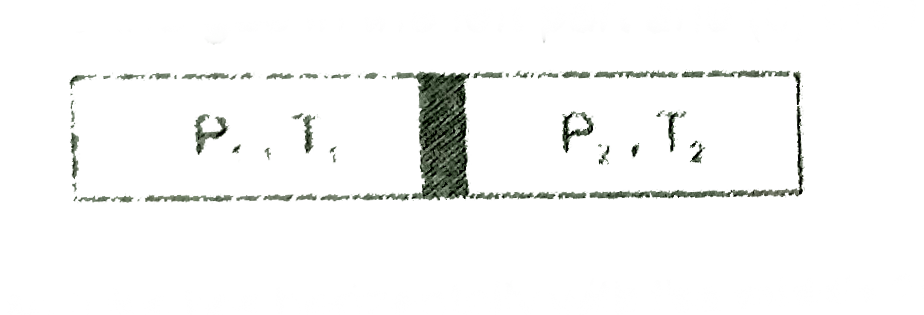
View SolutionShow a cylindrical tube of volume V_(0) divided in two parts by a frictionless separator. The walls of the tube are adiabatic but the separator is conducting, Ideal gases ate filled in the two parts. When the swparator is kept in the middle, the pressure are p_(1) and p-(2) in the left part and the right part respectively. The separator is slowly slid and is released at a position where it can stay in equilibrium. Find the volumes if the two parts. (figure)
View SolutionShows a cylindrical tube of length 30cm which is partitioned by a tight-fitting separator.The separator is very weakly conducting and can freely slide along the Tube. Ideal gases are filled in the two parts of the vessel. In the beginning, the temperature in the parts A and B are 400K and 100K respectively. The separator slides to a momentary equilibrium position of the separator,reached after a long time.

View Solution
