मान लो A={1,2,3,4,20} और R अर्थ का चार गुना है तब 4R1,8R2,12R3,16R4,20R5 अंत: A×A में। R={(4,1),(,8,2),(12,3),(16,4),(20,5)} जो A×A का उपसमुच्ये है।
Text Solution
मान लीजिएः A={1,3,5} एक परिमित समुच्ये है तो कार्तिकिये गुणनफल की परिभाषा के अनुसार-
A×A={(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5)}
इन योगो में हम निम्न प्रकार के सम्बन्दो की कल्पना कर सकते है।
(i) xR1y यदि x<y तो 1R13,1R15,3R15 अर्थार्त 1<3,1<5,3<5,R1 सम्बन्ध को संतुस्ट करने वले क्रमित युग्मो के समुच्ये को इस प्रकार लिखा जाता है।
R1={(1,3),(1,5),(3,5)}
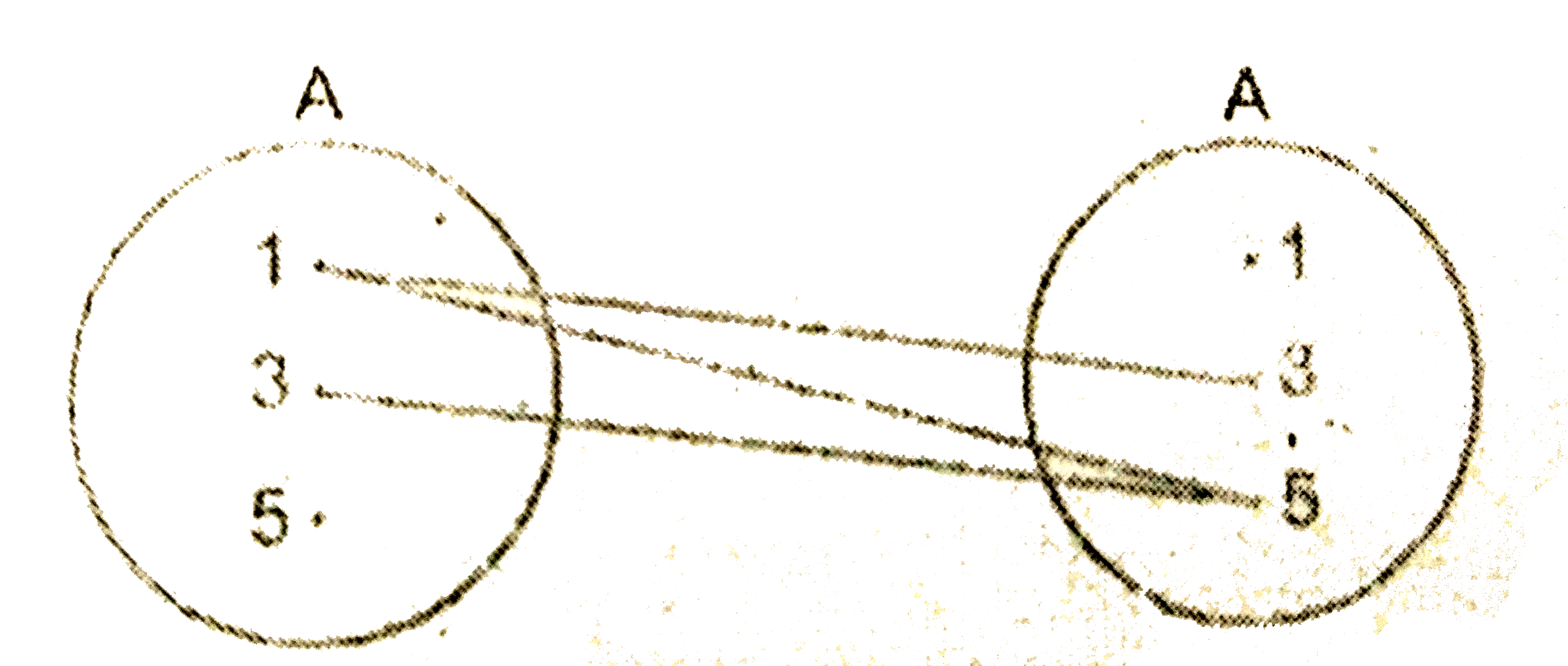
(ii)xR2Y यदि x=y, तो 1R21,3R23,5R25, अर्तार्थ 1=1,3=3, 5=5, अंत: R2={(1,1),(3,3),(5,5)}

(iii)xR3y यदि x>y, तो 3R3,5R31,5R33 तथा 3>1,5>1,5>3) अंत: R3={(3,1),(5,1),(5,3)}

तीनो स्थितियों से स्पस्ट है की-
R1⊆A×A,R2⊆A×AR3⊆A×A
|
Topper's Solved these Questions
- सम्बन्ध एवं फलनBOOK - MANOHAR RAYCHAPTER - सम्बन्ध एवं फलनEXERCISE - प्रशनावली 1(A)
3 Videos
- सम्बन्ध एवं फलनBOOK - MANOHAR RAYCHAPTER - सम्बन्ध एवं फलनEXERCISE - प्रश्नावली 1(A)
7 Videos
- समाकलनों के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - समाकलनों के अनुप्रयोग EXERCISE - प्रश्नावली 8 (C)
16 Videos
- सारणिक BOOK - MANOHAR RAYCHAPTER - सारणिक EXERCISE - प्रश्नावली 4(F)
26 Videos
Knowledge Check
An Aluminium (α=4×10−3K−1) resistance R1 and a carbon (α=−0.5×10−3K−1) resistance R2 are connected in series to have a resultant resistance of 36Ω at all temperatures. The values of R1 and R2 in Ω respectively are:
A32, 4B16, 20C4, 32D20, 16
