यूक्लिड की विभाजन एल्गोरिथ्म का प्रयोग करते हुए, ऐसी सबसे बड़ी संख्या ज्ञात कीजिए, जिससे 1251, 9377 और 15628 को भाग देने पर शेषफल क्रमशः 1, 2 और 3 प्राप्त हो ।
दिए गए शेषफलों को संख्याओं से घटाने पर प्राप्त संख्याएँ
1251−1=1250
9377−2=9375
और 15628−3=15625
यहाँ 1250<9375 है। 1250 और 9375 पर यूक्लिड प्रमेयिका का प्रयोग करने पर,
9375=1250×7+625
चूँकि शेषफल शून्य नहीं है, तब पुनः
1250=625×2+0
यहाँ शेषफल शून्य प्राप्त हो गया है।
अब 1250<15625
∴1250 और 15625 पर यूक्लिड प्रमेयिका का प्रयोग करने पर,
15625=1250×12+625
यहाँ शेषफल 625 प्राप्त हुआ ।
1250=625×2+0
अतः शेषफल शून्य प्राप्त हो गया है। दोनों ही स्थितियों में भाजक 625 प्राप्त हुआ है।
अतः बड़ी से बड़ी संख्या 625 है।
Topper's Solved these Questions
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(A)
15 Videos
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(B)
14 Videos
- बहुपद BOOK - MANOHAR RAYCHAPTER - बहुपद EXERCISE - प्रश्नावली 2(L)
21 Videos
- वृत्तBOOK - MANOHAR RAYCHAPTER - वृत्तEXERCISE - प्रश्नावली 10(C)
12 Videos
Similar Questions
निम्नलिखित संख्याओं का H.C.F ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथम का प्रयोग कीजिए -
(A) 135 और 225,
(B) 196 और 38220,
(C) 867 और 255
View Solutionनिन्मलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए -
(i) 140 (ii) 150 (iii) 3825 (iv) 5005 (v) 7429
View Solutionउपयुक्त सर्वसमिकाओं को प्रयोग करके निम्नलिखित गुणनफल ज्ञात कीजिए :
(i) (x+4)(x+10)
(ii) (x+8)(x−10)
(iii) (3x+4)(3x−5)
(iv) (y2+32)(y2−32)
(v) (3−2x)(3+2x)
View Solutionचित्र में, वृत्त का केन्द्र O है और AC वृत्त की स्पर्श रेखा है। यदि ∠ADB=55∘,तो ∠ACO की माप होगी :
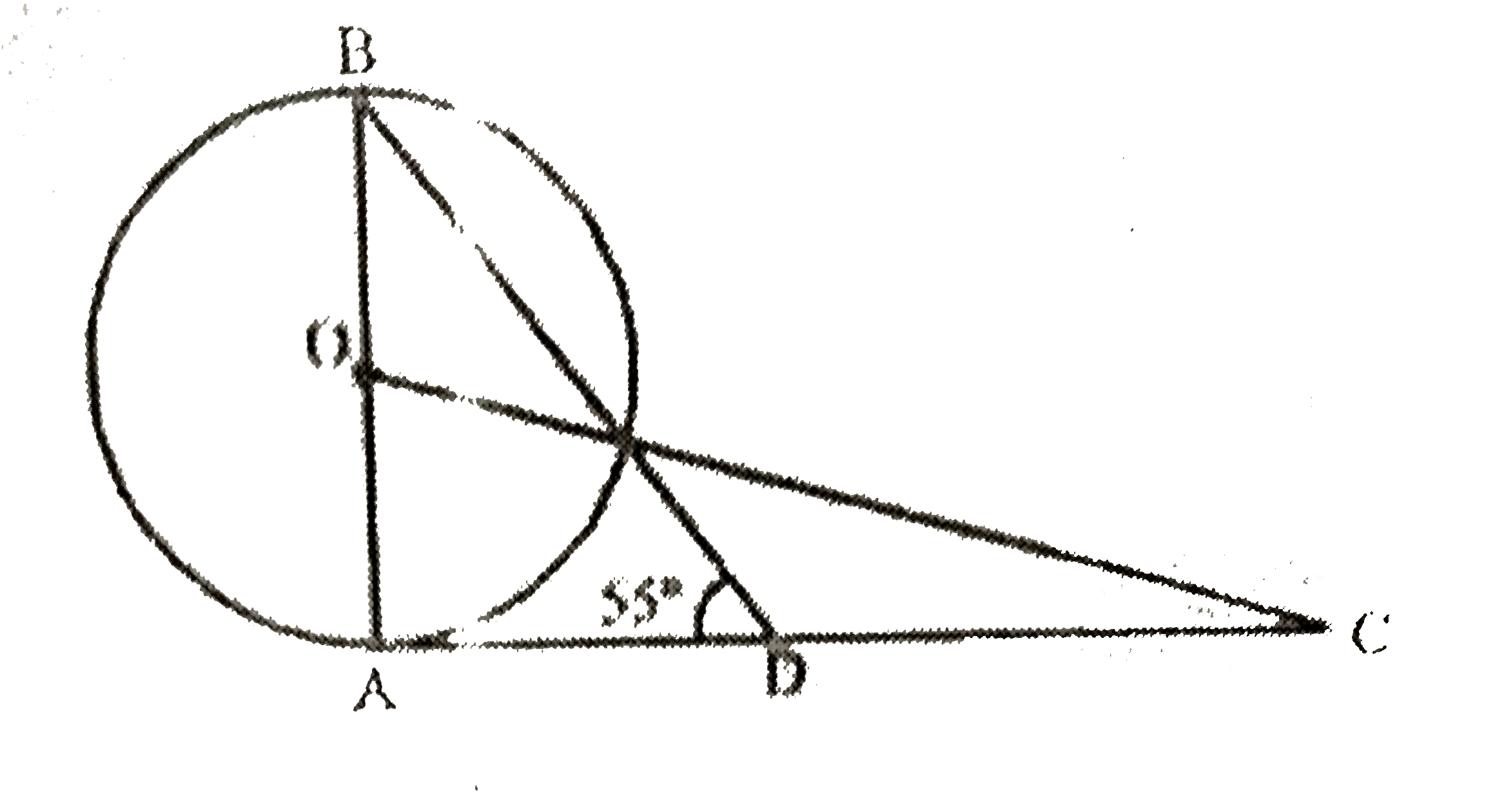
View Solutionवह सबसे बड़ी संख्या ज्ञात कीजिए जो 247 और 2055 को इस प्रकार विभाजित करती है कि प्र्त्येक स्थिति में शेषफल 7 प्राप्त हो।
View Solutionयूक्लिड विभाजन एल्गोरिथ्म | उदाहरण
View Solutionनिम्नलिखित संख्याओं का H.C.F. ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए :
36, 84
View Solutionनिम्नलिखित संख्याओं का H.C.F. ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए :
34, 102
View Solutionनिम्नलिखित संख्याओं का H.C.F. ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए :
45,75
View Solutionनिम्नलिखित संख्याओं का H.C.F. ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए :
112, 49
View Solutionx3−6x2+2x−4को x -1 से भाग देने पर प्राप्त होने वाला भागफल और शेषफल है :
View Solutionसंख्या पद्धति|यूक्लिड विभाजन प्रेमयिका|यूक्लिड विभाजन एल्गोरिथ्म|अभ्यास कार्य
View Solutionसंख्या पद्धति|यूक्लिड विभाजन प्रमेयिका (प्रेमय 1.1)|यूक्लिड विभाजन एल्गोरिथ्म|अभ्यास|सारांश
View Solutionसंख्या पद्धति|यूक्लिड विभाजन प्रमेयिका (प्रेमय 1.1)|यूक्लिड विभाजन एल्गोरिथ्म|अभ्यास कार्य|सारांश
View Solutionसंख्या पद्धति|यूक्लिड विभाजन प्रेमयिका|यूक्लिड विभाजन एल्गोरिथ्म|अंकगणित की आधारभूत प्रेमय|अभ्यास कार्य|सारांश
View Solutionसंख्या पद्धति|यूक्लिड विभाजन प्रमेयिका (प्रेमय 1.1)|यूक्लिड विभाजन एल्गोरिथ्म|अंकगणित की आधारभूत प्रेमय|अभ्यास कार्य|अपरिमेय संख्या|सारांश
View Solution
