दर्शाइए कि किसी धनात्मक पूर्णांक का वर्ग, किसी पूर्णांक q के लिए, 5q2 या 5q+3 के रूप का नहीं हो सकता ।
माना x कोई धनात्मक पूर्णांक है।
यूक्लिड की विभाजन प्रमेयिका द्वारा
x=5x+r,0≤r<5
इसलिए
x=5m,5m+1,5m+2,5m+3,5m+4,
जहाँ m पूर्ण संख्या है।
अब
x2=(5m)2=25m2=5(5m2)=5q. जहाँq=5m2
x2(5m+1)2=25m2+10m+1=5(5m2+2m)+1
=5q+1, जहाँ q=5m2+2m
x2=(5m+2)2=25m2+20m+4
=5(5m2+4m)+4=5q+4,जहाँq=5m2+4m
x2=(5m+3)2=25m2+30m+9=25m2+30m+5+4
=5(5m2+6m+1)+4=5q+4, जहाँq=5m2+6m+1
x2=(5m+4)2=25m2+40m+16=25m2+40m+15+1
=5(5m2+8m+3)+1=5q+1, जहाँ q=5m2+8m+3
अतः किसी धनात्मक पूर्णांक का वर्ग, किसी पूर्णांक q के लिए 5q+2 या 5q+3 के रूप का नहीं हो सकता है।
Topper's Solved these Questions
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(A)
15 Videos
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(B)
14 Videos
- बहुपद BOOK - MANOHAR RAYCHAPTER - बहुपद EXERCISE - प्रश्नावली 2(L)
21 Videos
- वृत्तBOOK - MANOHAR RAYCHAPTER - वृत्तEXERCISE - प्रश्नावली 10(C)
12 Videos
Similar Questions
निम्नलिखित संख्याओं का H.C.F ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथम का प्रयोग कीजिए -
(A) 135 और 225,
(B) 196 और 38220,
(C) 867 और 255
View Solutionनिन्मलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए -
(i) 140 (ii) 150 (iii) 3825 (iv) 5005 (v) 7429
View Solutionउपयुक्त सर्वसमिकाओं को प्रयोग करके निम्नलिखित गुणनफल ज्ञात कीजिए :
(i) (x+4)(x+10)
(ii) (x+8)(x−10)
(iii) (3x+4)(3x−5)
(iv) (y2+32)(y2−32)
(v) (3−2x)(3+2x)
View Solutionचित्र में, वृत्त का केन्द्र O है और AC वृत्त की स्पर्श रेखा है। यदि ∠ADB=55∘,तो ∠ACO की माप होगी :
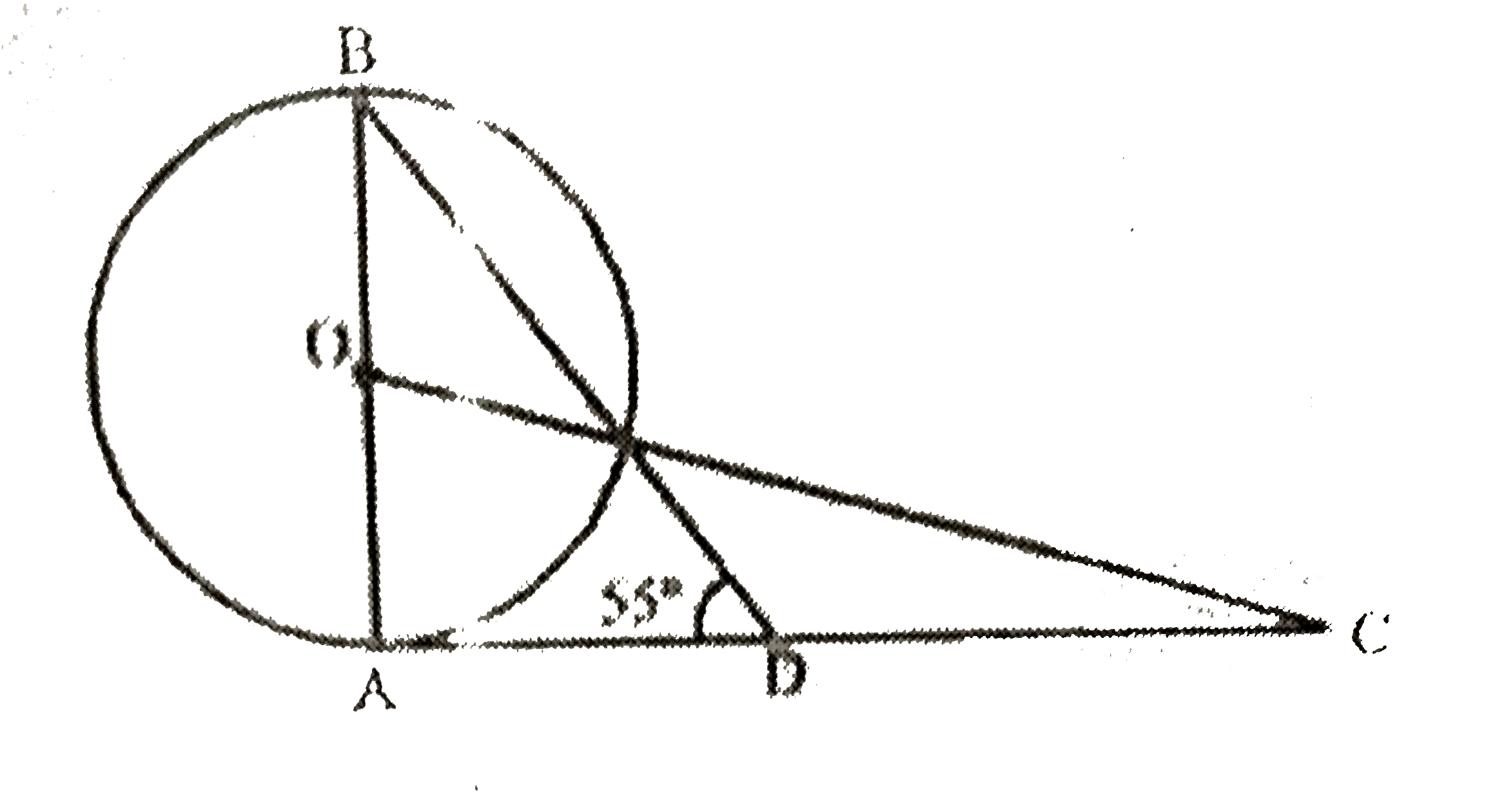
View Solutionमाना m ऐसा न्यूनतम धनात्मक पूर्णांक है की (1+x)2+(1+x)3+........+(1+x)49+(1+xm)50 के विस्तार में x2 का गुणांक (3n+1)51C3 किसी धनात्मक पूर्णांक n के लिए तब, n का मान है
View Solutionm के पूर्णांक मानों की संख्या, जिसके लिए रेखाओं 3x +4y= 9 तथा y=mx + 1 के प्रतिच्छेद बिन्दु का x-निर्देशांक भी पूर्णांक हो, है
View Solutionद्विपद प्रमेय किसी धन पूर्णांक n के लिए | महत्वपूर्ण प्रेक्षण | उदाहरण
View Solutionकिसी वर्ग के अंतराल 140-170 का वर्ग चिन्ह होगा :
View Solutionदर्शाइए कि धनात्मक सम पूर्णांक 4q या 4q+2 के रूप का होता है, जहाँ एक पूर्णाक है।
View Solutionपूर्णांक #!#पूर्णांकों का गुणन
View Solutionपूर्णांक#!#पूर्णांक के गुणन के गुण
View Solutionपूर्णांक #!#पूर्णांकों का विभाजन
View Solutionकिसी भी पूर्णांक घात के लिए द्विपद प्रमेय #!#उदाहरण
View Solutionवाइगोत्स्की के अनुसार किसी शब्द का अर्थ
View Solutionपढने का प्रारंभ____से ही हो और किसी उद्देश्य के लिए हो |
View Solutionपूर्णांक का परिचय#!#पूर्णांक का संख्या रेखा पर दर्शाना
View Solution
