दिखाइए कि √3 एक अपरिमेय संख्या है ।
इसके विपरीत हम यह मान ले कि √3 एक परिमेय संख्या है।
हम ऐसे दो पूर्णांक a और b(n≠0) प्राप्त कर सकते हैं कि √3=ab है।
यदि a और b में, 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखण्ड हो, तब उस उभयनिष्ठ गुणनखण्ड से भाग देकर a और b को सह अभाज्य बना सकते है।
अतः b√3=a है ।
दोनों पक्षों का वर्ग करने पर 3b2=a2 प्राप्त होता है।
अतः a2,3 से विभाजित है, तब 3, a को भी विभाजित करेगा।
अतः हम a=3c लिख सकते है, जहाँ c एक पूर्णांक है।
a के इस मान को 3b2=a2 में प्रतिस्थापित करने पर
3b2=9c2 या b2=3c2
इसका अर्थ है कि b2,3से विभाजित हो जाता है। इसलिए b भी उसे विभाजित होगा ।
अतः a और b में कम से कम एक उभयनिष्ठ गुणनखण्ड 3 है। परन्तु इससे इस तथ्य का विरोधाभास होता है कि a और b सह अभाज्य है।
इसलिए यह विरोधाभास हमारी कल्पना की कमी के कारण है कि √3 एक परिमेय संख्या है ।
अतः√3 एक अपरिमेय संख्या है।
Topper's Solved these Questions
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(A)
15 Videos
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(B)
14 Videos
- बहुपद BOOK - MANOHAR RAYCHAPTER - बहुपद EXERCISE - प्रश्नावली 2(L)
21 Videos
- वृत्तBOOK - MANOHAR RAYCHAPTER - वृत्तEXERCISE - प्रश्नावली 10(C)
12 Videos
Similar Questions
निम्नलिखित संख्याओं का H.C.F ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथम का प्रयोग कीजिए -
(A) 135 और 225,
(B) 196 और 38220,
(C) 867 और 255
View Solutionनिन्मलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए -
(i) 140 (ii) 150 (iii) 3825 (iv) 5005 (v) 7429
View Solutionउपयुक्त सर्वसमिकाओं को प्रयोग करके निम्नलिखित गुणनफल ज्ञात कीजिए :
(i) (x+4)(x+10)
(ii) (x+8)(x−10)
(iii) (3x+4)(3x−5)
(iv) (y2+32)(y2−32)
(v) (3−2x)(3+2x)
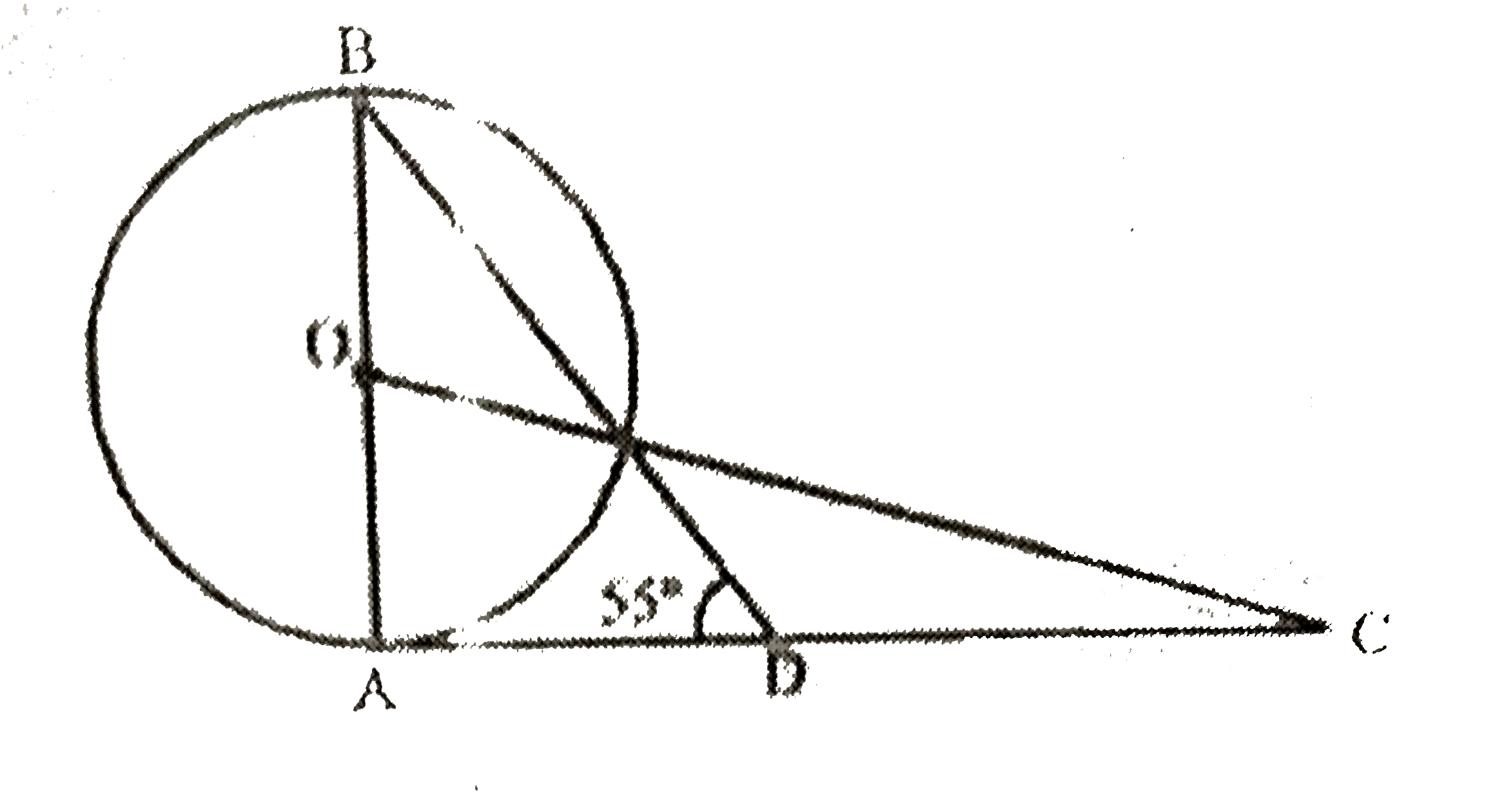
View Solutionचित्र में, वृत्त का केन्द्र O है और AC वृत्त की स्पर्श रेखा है। यदि ∠ADB=55∘,तो ∠ACO की माप होगी :
View Solutionसमुच्चय {x:x एक अभाज्य संख्या, जो कि संख्या 30 की भाजक है } को रोस्टर रूप में लिखिय।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionनिम्नलिखित संख्याओं में अपरिमेय संख्या कौन-सी है ?
View Solutionनिम्न में कौन-सी अपरिमेय संख्या है ?
View Solutionनिम्न में से कौन-सी अपरिमेय संख्या है ?
View Solutionदर्शाइए कि 7sqrt(3) एक अपरिमेय संख्या है।
[H.B. 2012 Set C]
View Solutionसिद्ध कीजिए कि 3-2sqrt(5) एक अपरिमेय संख्या है।
[H.B. 2017, Set B]
View Solutionदिखाइए कि अनुक्रम जिसका n वाँ पद 2n2+n+1 है, एक A.P. नहीं है।
View Solutionसिद्ध कीजिये कि3−2√5 एक अपरिमेय संख्या है।
View Solutionनिम्नलिखित कथनो में सत्य एवं असत्य कथन की पहचान करे (2sqrt5)/(3sqrt15) एक अपरिमेय संख्या है
View SolutionRevision|संख्या पद्दती#!#अपरिमेय संख्या#!#वास्तविक संख्या और उनके दशमलव
View Solutionसंख्या पद्धति|अभ्यास कार्य|अपरिमेय संख्या|वास्तविक संख्या|संख्या रेखा पर अपरिमेय संख्या का निरूपण|सारांश
View Solution
