सिद्ध कीजिए कि ऐसी किसी परिमेय संख्या का घन नहीं है ?
अन्तर्विरोध के रूप में मान लीजिए कि एक परिमेय संख्या pq ऐसी है कि (pq)3=7 क्योंकि 13=1 और 23=8, इसलिए निष्कर्ष निकलता है कि 1<pq<2 और q=1 लें तो pq एक पूर्णांक होगा, लेकिन 1 और 2 के बीच कोई पूर्णांक नहीं है।
माना कि p और q का कोई सार्वभाजक नहीं है, क्योंकि यदि ऐसा हो, तो हर और अंश दोनों को उससे भाग देने पर नये रूप में अंश और हर का कोई सार्वभाजक नहीं होगा।
अब 7=p3q3
दोनों पक्षों को q2 से गुणा करने पर
7q2=p3q
क्योकि q एक पूर्णांक है इसलिए 7q2 भी एक पूर्णांक होगा| क्योंकि q तथा q का कोई सार्वभाजक नहीं है, इसलिए q और p3 का भी कोई सार्वभाजक होगा। क्योंकि q>1 इसलिए p3q एक भिन्न होगी जो किसी पूर्णांक के बराबर नहीं है।
अतः 7q2≠p3q
इस अन्तर्विरोध से कथन सिद्ध हो जाता है।
Topper's Solved these Questions
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(A)
15 Videos
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(B)
14 Videos
- बहुपद BOOK - MANOHAR RAYCHAPTER - बहुपद EXERCISE - प्रश्नावली 2(L)
21 Videos
- वृत्तBOOK - MANOHAR RAYCHAPTER - वृत्तEXERCISE - प्रश्नावली 10(C)
12 Videos
Similar Questions
निम्नलिखित संख्याओं का H.C.F ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथम का प्रयोग कीजिए -
(A) 135 और 225,
(B) 196 और 38220,
(C) 867 और 255
View Solutionनिन्मलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए -
(i) 140 (ii) 150 (iii) 3825 (iv) 5005 (v) 7429
View Solutionउपयुक्त सर्वसमिकाओं को प्रयोग करके निम्नलिखित गुणनफल ज्ञात कीजिए :
(i) (x+4)(x+10)
(ii) (x+8)(x−10)
(iii) (3x+4)(3x−5)
(iv) (y2+32)(y2−32)
(v) (3−2x)(3+2x)
View Solutionचित्र में, वृत्त का केन्द्र O है और AC वृत्त की स्पर्श रेखा है। यदि ∠ADB=55∘,तो ∠ACO की माप होगी :
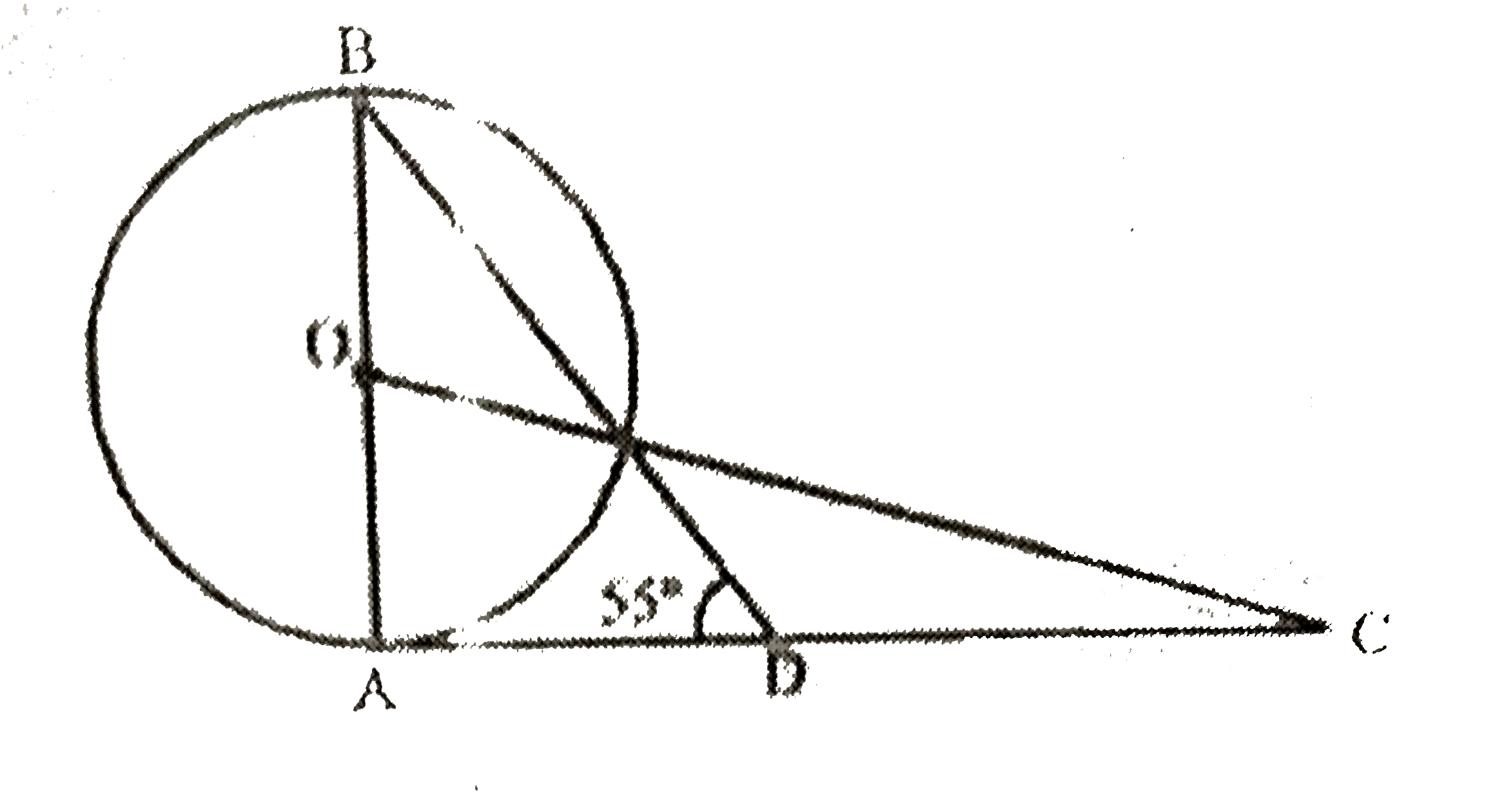
View Solutionनीचे दर्शाये दशमलव प्रसार के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नही। यदि यह परिमेय संख्या है, तो इसके हर के अभाज्य गुणनखंडन के बारे में अपनी टिप्पणी लिखिए-
27.¯¯¯¯¯¯¯¯¯¯¯¯143857
View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionमाना z1=10+6i और z2=4+6i यदि सम्मिश्र संख्या z इस प्रकार है कि (z−z1)(z−z2) का कोणांक π4 है, तो सिद्ध कीजिए कि |z−7−9i|=3√2.
View Solutionपरिमेय संख्याओं का परिचय | परिमेय संख्या के गुणधर्म (भाग 1)
View Solutionपरिमेय संख्याओं का संख्या रेखा पर निरूपण
View Solutionनिम्न में से कौन-सी परिमेय संख्या नहीं है ?
View Solutionनिम्न में से कौन-सी परिमेय संख्या नहीं है ?
View Solutionकिसी घन संख्या का घनमूल
View Solutionअपरिमेय संख्याएँ |परिमेय संख्या का दशमलव प्रसार
View Solution
