सिद्ध कीजिए कि एक 5−2√3 अपरिमेय संख्या है।
इसके विपरीत मान लीजिए कि 5−2√3 एक परिमेय संख्या है अर्थात सह अभाज्य ऐसी संख्याएँ a और b(b≠0) ज्ञात कर सकते है कि
5−2√3=ab
या 2√3=5−ab
या √3=5b−a2b
∵ a तथा b पूर्णांक है, ∴5b−a2b एक परिमेय संख्या है।
अर्थात √3 एक परिमेय संख्या है।
परन्तु इस तथ्य का विरोधाभास प्राप्त होता है कि √3 एक अपरिमेय संख्या है
अतः 5−2√3 एक अपरिमेय संख्या होगी।
Topper's Solved these Questions
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(A)
15 Videos
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(B)
14 Videos
- बहुपद BOOK - MANOHAR RAYCHAPTER - बहुपद EXERCISE - प्रश्नावली 2(L)
21 Videos
- वृत्तBOOK - MANOHAR RAYCHAPTER - वृत्तEXERCISE - प्रश्नावली 10(C)
12 Videos
Similar Questions
निम्नलिखित संख्याओं का H.C.F ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथम का प्रयोग कीजिए -
(A) 135 और 225,
(B) 196 और 38220,
(C) 867 और 255
View Solutionनिन्मलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए -
(i) 140 (ii) 150 (iii) 3825 (iv) 5005 (v) 7429
View Solutionउपयुक्त सर्वसमिकाओं को प्रयोग करके निम्नलिखित गुणनफल ज्ञात कीजिए :
(i) (x+4)(x+10)
(ii) (x+8)(x−10)
(iii) (3x+4)(3x−5)
(iv) (y2+32)(y2−32)
(v) (3−2x)(3+2x)
View Solutionचित्र में, वृत्त का केन्द्र O है और AC वृत्त की स्पर्श रेखा है। यदि ∠ADB=55∘,तो ∠ACO की माप होगी :
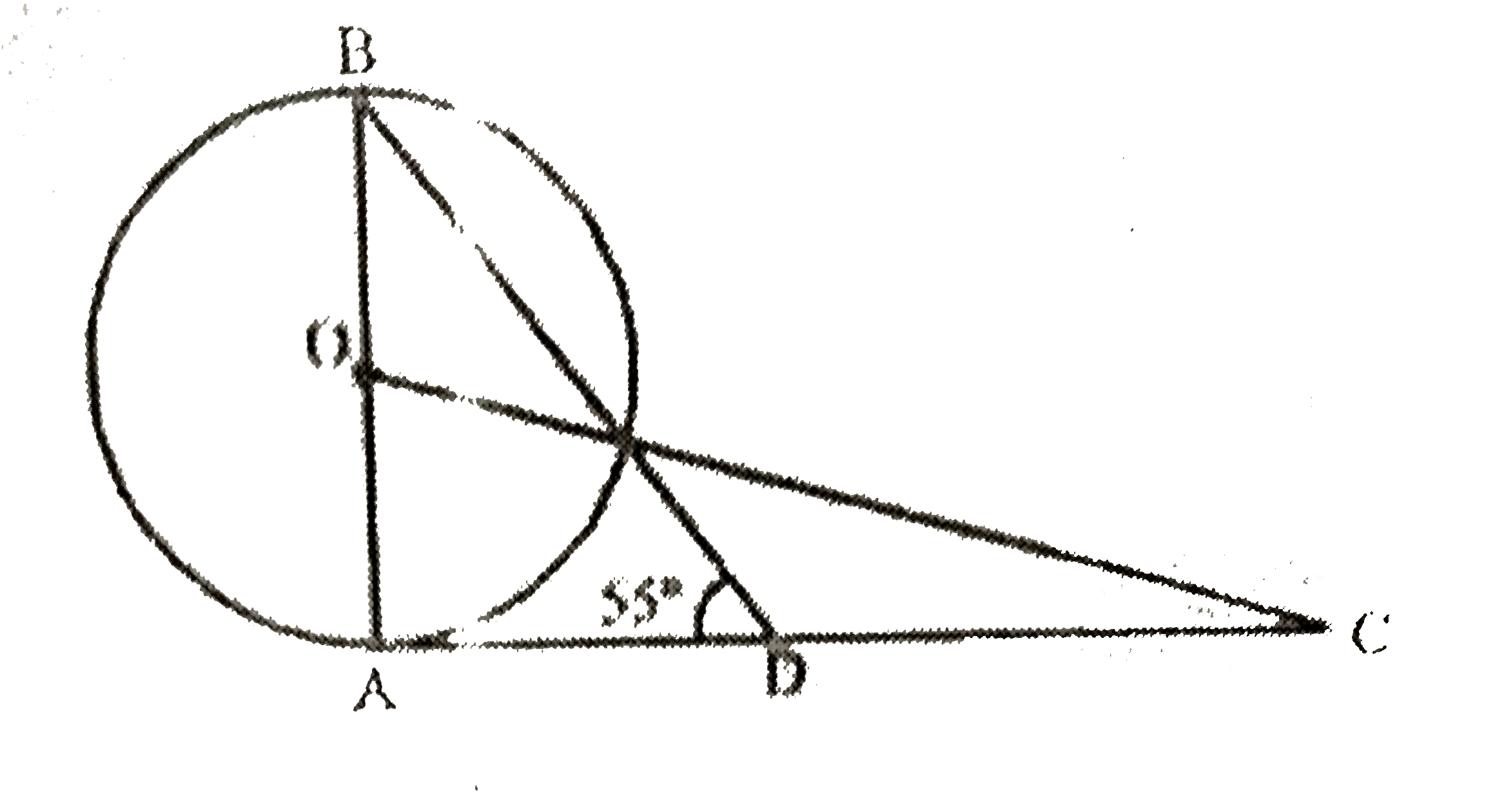
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionसिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय संख्याएँ है-
32√5
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि f(x)=ax,o<a<1,R में ह्रासमान है।
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solutionसिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसरे पास पर 6 आने कि स्वतन्त्र घटनाएँ है।
View Solutionनिम्न में कौन-सी अपरिमेय संख्या है ?
View Solutionदर्शाइए कि 7sqrt(3) एक अपरिमेय संख्या है।
[H.B. 2012 Set C]
View Solutionसिद्ध कीजिए कि 3-2sqrt(5) एक अपरिमेय संख्या है।
[H.B. 2017, Set B]
View Solution