A manufacturer can sell x items at the price of Rs. (330−x) each. The cost of producing xitems is Rs. x2+10x−12. How many items must be sold so that his profit is maximum?
The correct Answer is:80
Step by step video, text & image solution for A manufacturer can sell x items at the price of Rs. (330-x) each. The cost of producing xitems is Rs. x^2+ 10x-12. How many items must be sold so that his profit is maximum? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DERIVATIVES EXERCISE - MULTIPLE CHOICE QUESTIONS
12 Videos
- APPLICATIONS OF DERIVATIVES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DERIVATIVES EXERCISE - MULTIPLE CHOICE QUESTIONS
12 Videos
- APPLICATIONS OF DEFINITE INTEGRALS ( AREA ) BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS ( AREA ) EXERCISE - EXAMPLES FOR PRACTICE (3 OR 4 MARKS )
5 Videos
- BINOMIAL DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - BINOMIAL DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
A manufacturer can sell 'x' items at a price of Rs (250−x) each. The cost of producing 'x' items is Rs (x2−50x+12). Determine the number of items to be sold so that he can make maximum profit.
View SolutionA manufacturer can sell x items at a price of Rs. (5−x100) each. The cost price of x items is Rs. (x5+ 500). Find the number of items he should sell to earn maximum profit.
View Solution
Knowledge Check
Manufacturer can sell x items at a price of rupees (5−x100)each. The cost price of x items is Rs (x5+500). Find the number of items he should sell to earn maximum profit
Ax=140Bx=240Cx=340Dx=440Total cost of producing x items is Rs(x2+10x+12) and selling price of each is Rs(330−x) . Then output for maximum profit must be
A50B60C70D80
A manufacturer can sell x items per month at a price p= Rs.(300-2x) Manufacturer's cost of production, Rs.y, of x items is given by y=2x+1000 . Find the number of items to be produced per month to yield the maximum profit.
View SolutionA factory can shell 'x' items per week at price of Rs (20−x1000) each. If the cost price of one item is Rs (5+2000x), find the number of items, the factory should produce every week for maximum profit. If price is reduced, how it will effect the sale? Give reasons.
(ii) Profit function of a company is given as :
P(x)=24x5−x2100−500.
where 'x' is the number of units produced.
What is the maximum profit of the company?
View SolutionA producer can sell any quantity of a commodity at a given price of Rs. 10 per unit. His cost schedule is given below:
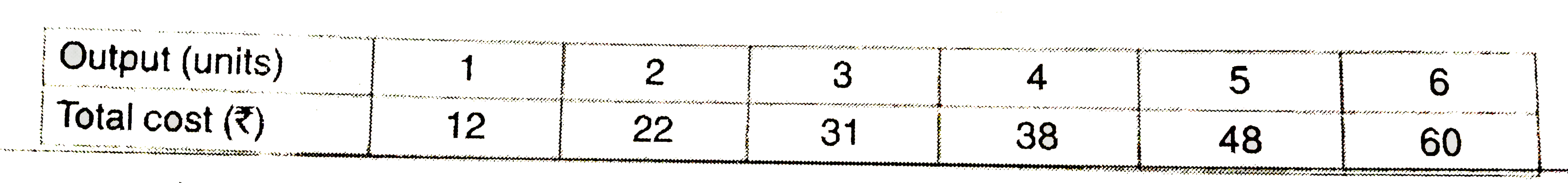
How many units should he produce to get maximum profit ? Explain.
View SolutionA manufacturing company produces x items at a total cost of Rs 40+2x. Their price per item is given as p=120−x Find the value of x for which (i) revenue is increasing (ii) profit is increasing
Also find elasticity of demand for price Rs. 80.
View SolutionThe manufacturer of a certain item can sell all he can produce at the selling price of Rs. 60 each. It costs him Rs. 40 in materials and labour to produce each item and he has overhead expenses of Rs. 3000 per week in order to operate the plant. The number of units he should produce and sell in order to make a profit of at least Rs. 1000 per week, is 200 b. 300 c. 250 d. 400
View SolutionA manufacturer of a certain item can sell all he can produce at the selling price of Rs 60 each. It costs him Rs 40 in materials and labour to produce each item and he has overhead expenses of Rs 3000 per week in order to operate that plant. The number of units he should produce and sell in order to make a profit of at least Rs 1000 per week is
View Solution
