The probability distribution of a random variable X is as below:

(1) Construct c.d.f F(x) of X.
(2) obtain P(X≤0.5),F(−0.5),F(2),P(X≤4)
Text Solution
(1) By the defintion of c.d.f
F(x)=P(X≤x)
∴F(−1.5)=P(X≤−1.5)=0.05
F(−1.5)=P(X≤−0.5)=P(X=−1.5)+P(X=−0.5)
=0.05+0.2=0.25
F(0.5)=P(X≤0.5)=P(X=−1.5)+P(X=−0.5)+P(X=0.5)
0.05+0.2+0.15=0.4
F(1.5)=P(X≤1.5)=P(X=−1.5)+P(X=−0.5)+P(X=0.5)+P(X=1.5)
=0.05+0.2+0.15+0.25=0.65
F(2.5)=P(X≤2.5)=P(X=−1.5)+P(X=−0.5)+P(X=0.5)+P(X=1.5)+P(x=2.5)
=0.05+0.2+0.15+0.25+0.35=1
Hence the c.d.f of X is as follow:

(2) P(X≤0.5)=F(0.5)=0.4
f(−0.5)=0.25,F(2)=P(X≤2)=P(X≤1.5)=F(1.5)=0.65
P(X≤4)=F(4)=1 ....[∵F(X)=1for any x≤2.5]
|
Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - EXAMPLE FOR PRACTICE
20 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- PLANE BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PLANE EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - BINOMIAL DISTRIBUTION
20 Videos
Similar Questions
Knowledge Check
If the probability density function of a random variable X is f(x)=x2 in 0≤x≤2, then P(X>1.5∣X>1) is equal to
A716B34C712D2164The p.d.f of a continuous random variable X is f(x)=x23,−1<x<2 0 = otherwise Then the c.d.f of X is
Ax39+19Bx39−19Cx24+14D19x3+19If the p.d.f of a random variable X is
F(x)={0.5x0≤x≤20otherwise
Then the value of P(0.5≤X≤1.5) isA14B12C34D1
If p.d.f, of continuous random variable X is f(x)={2x3;0≤x≤10; otherwise. Find P(X≤0.5)andP(0.5≤X≤1)
View SolutionLet X be a continuous random variable with p.d.f. f(x) = kx(1-x), 0b).. find k and determine anumber b such that P(X≤b) = P(X≥b)
View SolutionThe following is the c.d.f. of r.v. X
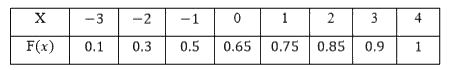
Find (i) P(−1≤X≤2) (ii) P(X≤3/X>0).
View SolutionA random variable X has the probability distribution:

For the events E = (X is prime number) and F = {X < 4}, the probability P(E∪F) is
View SolutionX is continuous random variable with probability density function f(x)=x28,0≤x≤1. Then, the value of P(0.2≤X≤0.5) is
View Solution

