State the expression for the moment of inertia of a solid cylinder of uniform cross section about an axis through its centre and perpendicular to its length.
To find the expression for the moment of inertia of a solid cylinder of uniform cross-section about an axis through its center and perpendicular to its length, we can follow these steps:
1. Understand the Geometry of the Cylinder:
- Consider a solid cylinder with mass m and radius r. The axis of rotation is through the center of the cylinder and perpendicular to its length.
2. Use the Formula for Moment of Inertia:
- The moment of inertia I about an axis through the center of mass for a solid cylinder is given by the formula:
I=12mr2
- This formula is derived from integrating the contributions of all the mass elements of the cylinder.
3. Derivation (Optional):
- If we were to derive it, we would consider a differential mass element dm at a distance r from the axis of rotation. The moment of inertia of this element is given by:
dI=r2dm
- To find the total moment of inertia, we would integrate this expression over the entire volume of the cylinder.
4. Final Expression:
- Thus, the moment of inertia of a solid cylinder about an axis through its center and perpendicular to its length is:
I=12mr2
- Consider a solid cylinder with mass m and radius r. The axis of rotation is through the center of the cylinder and perpendicular to its length.
- The moment of inertia I about an axis through the center of mass for a solid cylinder is given by the formula:
I=12mr2
- This formula is derived from integrating the contributions of all the mass elements of the cylinder.
- If we were to derive it, we would consider a differential mass element dm at a distance r from the axis of rotation. The moment of inertia of this element is given by:
dI=r2dm
- To find the total moment of inertia, we would integrate this expression over the entire volume of the cylinder.
- Thus, the moment of inertia of a solid cylinder about an axis through its center and perpendicular to its length is:
I=12mr2
Topper's Solved these Questions
- VERY SHORT ANSWER QUESTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VERY SHORT ANSWER QUESTIONS EXERCISE - OSCILLATIONS
11 Videos
- VERY SHORT ANSWER QUESTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VERY SHORT ANSWER QUESTIONS EXERCISE - ELASTICITY
9 Videos
- VERY SHORT ANSWER QUESTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VERY SHORT ANSWER QUESTIONS EXERCISE - GRAVITATION
11 Videos
- SOLVED PROBLEMS-II BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SOLVED PROBLEMS-II EXERCISE - Assignments
5 Videos
Similar Questions
The moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionState an expression for the moment of inertia of a solid uniform disc rotating about an axis passing through its centre, perpendicular to its plane. Hence derive an expression for the moment of inertia and radius of gyration.
(i) about a tangent in the plane of the disc, and
(ii) about a tangent perpendicular to the plane of the disc. In a set, 21 tuning forks are arranged in a series of decresing frequencies. Each tuning fork produces 4 beats per second with the preceding fork. If the first fork is an octave of the last fork , find the frequencies of the first and tenth forks.
View Solution
Knowledge Check
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correctMoment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
AI=12MR2BI=MR2CI=32MR2DI=52MR2Find the moment of inertia of a circular disk or solid cylinder of radius R about the axis through the centre and perpendicular to the flat surface.
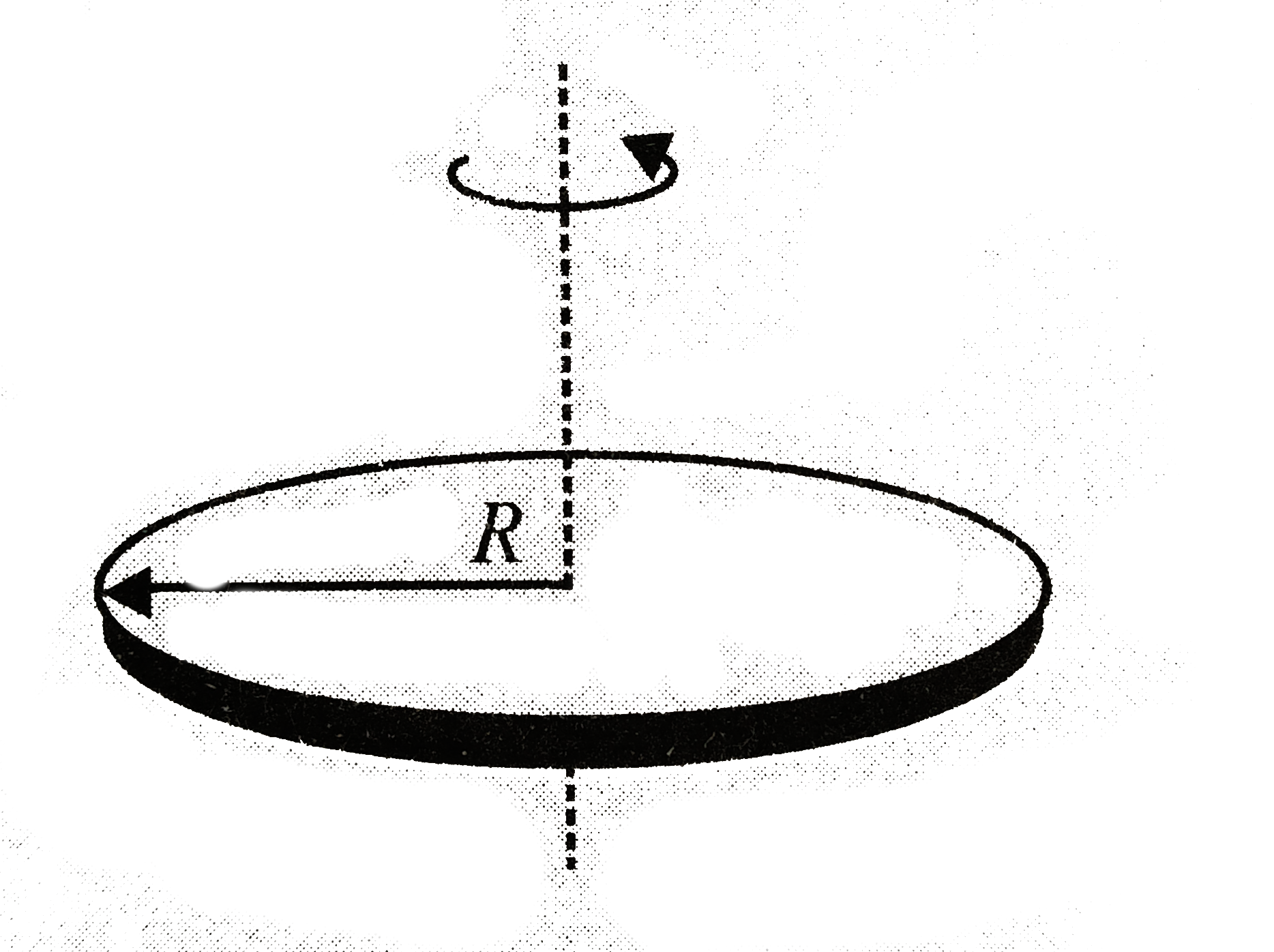 A12MR2B23MR2C32MR2DMR2
A12MR2B23MR2C32MR2DMR2
Derive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through its center and perpendicular to its plane will

View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionThe radius of gyration of an uniform rod of length L about an axis passing through its centre of mass and perpendicular to its length is.
View Solution
