Question

When light passes from a denser medium to a rarer medium

Explanation

Consider a plane wavefront of monochromatic light incident obliquely on a plane mirror PQ. `A_(1)B_(1)` and AB are the successive positions of the incident wavefront one wavelength apart, `A_(1)A and B_(1)B` are the corresponding incident rays of light.
When the wavefront AB is incident on the mirror, at first, point A becomes a secondary source and emits secondary waves in the same medium. Let v be the speed of light in the medium.

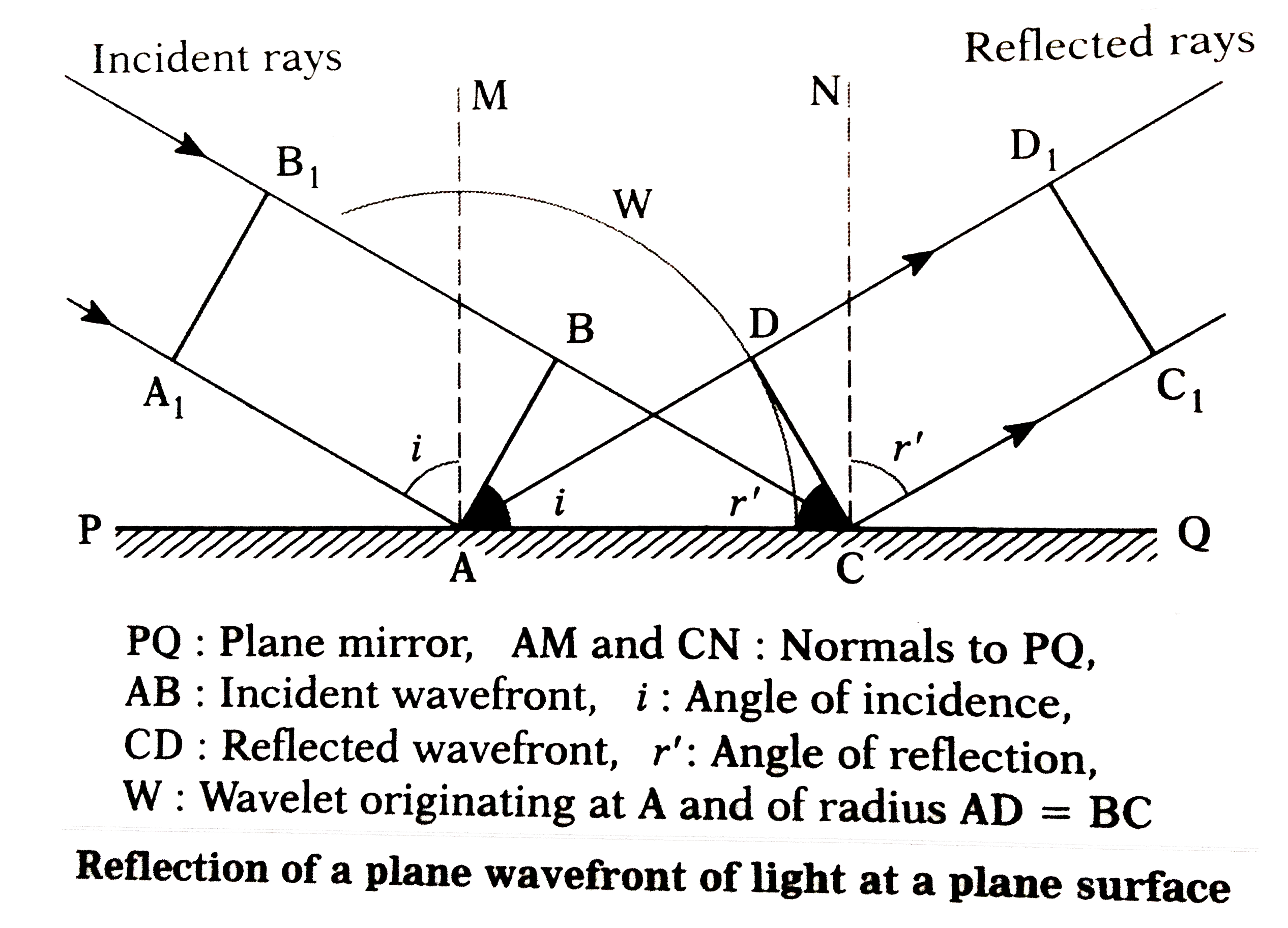
If t is the time taken by the incident wavefront to travel from B to C, then BC= vt. During this time secondary waves originating at A cover the same distance, so that the secondary spherical wavelet has a radius vt.
With A as the centre, draw a hemisphere of radius vt, to represent the secondary wavelet originating from A. Draw a tangent CD to the secondary wavelet.
As all points on CD are in the same phase of wave motion, CD represents the reflected wavefront. It travels parallel to itself taking successive positions `C_(1)D_(1)`, etc. one wavelength apart. Therefore, `AD_(2) and C C_(2)` represent the reflected rays. If a normal AN is drawn to PQ, `angle A_(1)AM=i=` angle of incidence and `angle MAD=r'=`angle of reflection.
In `triangle ABC and triangle ADC, AC` is common, AD = BC = vt and
`angle ABC = angle ADC =90^(@)`
`therefore triangle ABC and triangle ADC` are congruent.
`therefore angle BAC =angle DCA " " `...(1)
From the figure, `angle A_(1)AM+angle MAB=90^(@) and angle MAB +angleBAC=90^(@)`
`therefore angle BAc=angle A_(1)AM=i " "` ...(2)
Also, `angle MAD +angle DAC =90^(@) and angle DAC+angle DCA=90^(@)`
`therefore angle DCA=angle MAD=r' " " ` ...(3)
`therefore From Eqs. (1), (2) and (3), i = r'
Thus, the laws of angle of incidence is equal to the angle of reflection. Also, it can be seen from the figure that the incident ray and the reflected ray lie on the opposite sides of the normal to the reflecting surface at the point of incidence and all of them lie in the same plane.
Thus, the laws of reflection of light can be deduced from huygens' wave theory.