Obtain an expression for path difference and frinage width of interfereance pattern in Young's double slit experiment. Show that the fring width is same for consecutive bright and dark bands.
The refractive indices of glass and water w.r.t. air are $\frac{3}{2} and \frac{4}{3}$ respectively. Determine the refractive index of glass w.r.t. water.

Video Solution

Text Solution

Verified by Experts

Consider Young's double-slit experimental setup. Two narrow coherent light sources are obtained by wavefront splitting as monochromatic light of wavelength $λ$ emerges out of two closely spaced slits $S_{1} and S_{2}$ as shown in the figure. The separation $S_{1} S_{2} = d$ is very small. The interference pattern is observed on a screen placed parallel to the plane of $S_{1} S_{2}$ and some considerable distance $D (D > > d)$ from the slits. OP is the two light waves from $S_{1} and S_{2}$ reach Q along the paths $S_{1} Q and S_{2} Q,$ respectively.

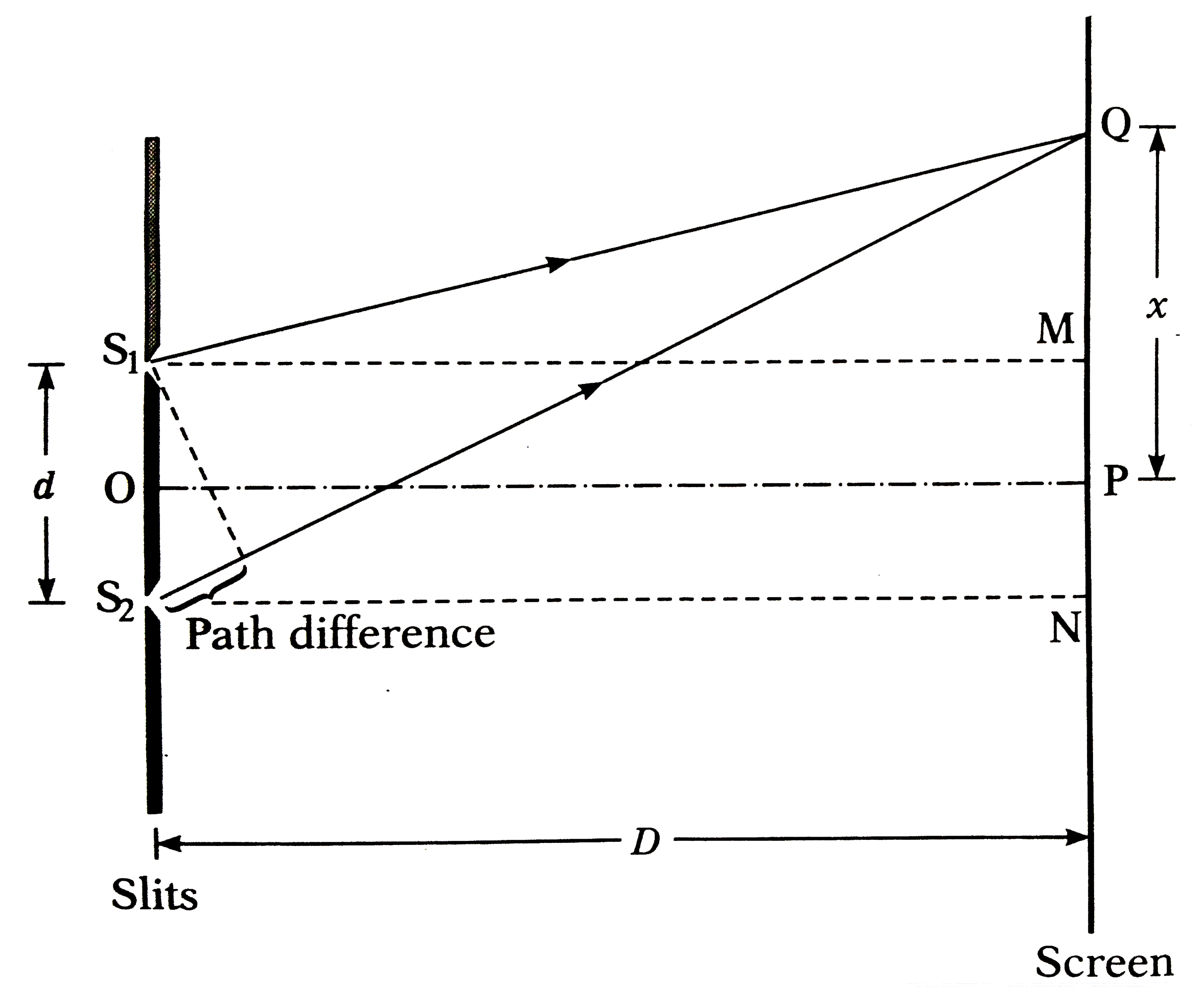
From the figure,
${(S_{2} Q)}_{2}^{2} = {(S_{2} N)}_{2}^{2} + {(Q N)}^{2} = {(S_{2} N)}_{2}^{2} + {(Q P + P N)}^{2}$
$= D^{2} + {(x + \frac{d}{2})}^{2} = D^{2} + x^{2} + x d + \frac{d^{2}}{4}$ ...(1)
$and {(S_{1} Q)}_{1}^{2} = {(S_{1} M)}_{1}^{2} + {(Q M)}^{2}$
$= {(S_{1} M)}_{1}^{2} + {(Q P - M P)}^{2}$
$= D^{2} + {(x - \frac{d}{2})}^{2} = D^{2} + x^{2} - x d + \frac{d^{2}}{4}$ ...(2)
$∴ {(S_{2} Q)}_{2}^{2} - {(S_{1} Q)}_{1}^{2} = 2 x d$ ...(3)
$∴ (S_{2} Q + S_{1} Q) (S_{2} Q - S_{1} Q) = 2 x d$
$∴ S_{2} Q - S_{1} Q = \frac{2 x d}{S_{2} Q + S_{1} Q}$
In practice, D gtgt x and D gtgt d, so that $S_{2} Q + S_{1} Q ≅ 2 D$
$∴$ Path difference, $(S_{2} Q - S_{1} Q) ≅ \frac{2 x d}{2 d} = \frac{x d}{D}$ ...(4)
Point Q will be bright ( maximum intensity), if the path difference, $\frac{x d}{D} = n l m b d a,$
where n = 0, 1, 2, 3, ...... .
Point Q will be dark (minimum intensity ), if $\frac{x d}{D} = (2 m - 1) \frac{λ}{2},$
where m = 1, 2, 3, .... .
Fpr point P, the path difference $(S_{2} P - S_{1} P) = 0 .$ Hence, point P will be bright, corresponding to the central bright fringe or band. On both sides of point P, the interference pattern consists of alternate bright and dark bands of fringes parrellel to the slit for path difference $n λ and (m - \frac{1}{2}) λ,$ respectively, as n and m take values 1, 2, 3, ....... .
Let $x_{n} and x_{n + 1}$ be the distances of the nth and (n + 1)th successive bright fringes from the central bright fringe.
$∴ \frac{x_{n} d}{D} = n λ or x_{n} = \frac{n λ D}{d}$
$and \frac{x_{n + 1} d}{D} = (n + 1) λ or x_{n + 1} = \frac{(n + 1) λ D}{d}$
$∴$ The distance between consecutive bright fringes, i.e., the fringe width,
$X = x_{n + 1} - x_{n} = \frac{λ D}{d} [(n + 1) - n] = \frac{λ D}{d}$
For successive dark fringes.
$X = x_{m + 1} - x_{m} = \frac{λ D}{d} [m + \frac{1}{2} - (m - \frac{1}{2})] = \frac{λ D}{d},$
which is the same as in the case of bright fringes.

Updated on:21/07/2023

The refractive indices of glass and water with respect to air are 3/2 and 4/3 respectively. The refractive index of glass w.r.t. water will be
A $\frac{8}{9}$
B $\frac{9}{8}$
C $\frac{7}{6}$
DNone of these
The refractive indices of glass and water with respect to air $\frac{1}{2} and \frac{1}{\sqrt{3}}$ respectively. Then the refractive index of are glass with respect to water is
A $\frac{1}{\sqrt{3}}$
B $\frac{\sqrt{3}}{2}$
C $\frac{2}{\sqrt{3}}$
D2
The refractive indices of glass and water are $\frac{3}{2}$ and $\frac{4}{3}$ respectively. The refractive index of glass with respect to water is
A2
B $\frac{8}{9}$
C $\frac{9}{8}$
D $\frac{5}{3}$