Question

Show that linear SHM is the projection of a uniform circular motion on any diameter.

Explanation

Consider a particle which moves with a constant angular speed `omega` around a circular path of radius A. Let the path lie in the x-y plane with the centre at the origin O. The instantaneous position Q of the particle is called the reference point and the circle in which the particle moves is called the reference circle.

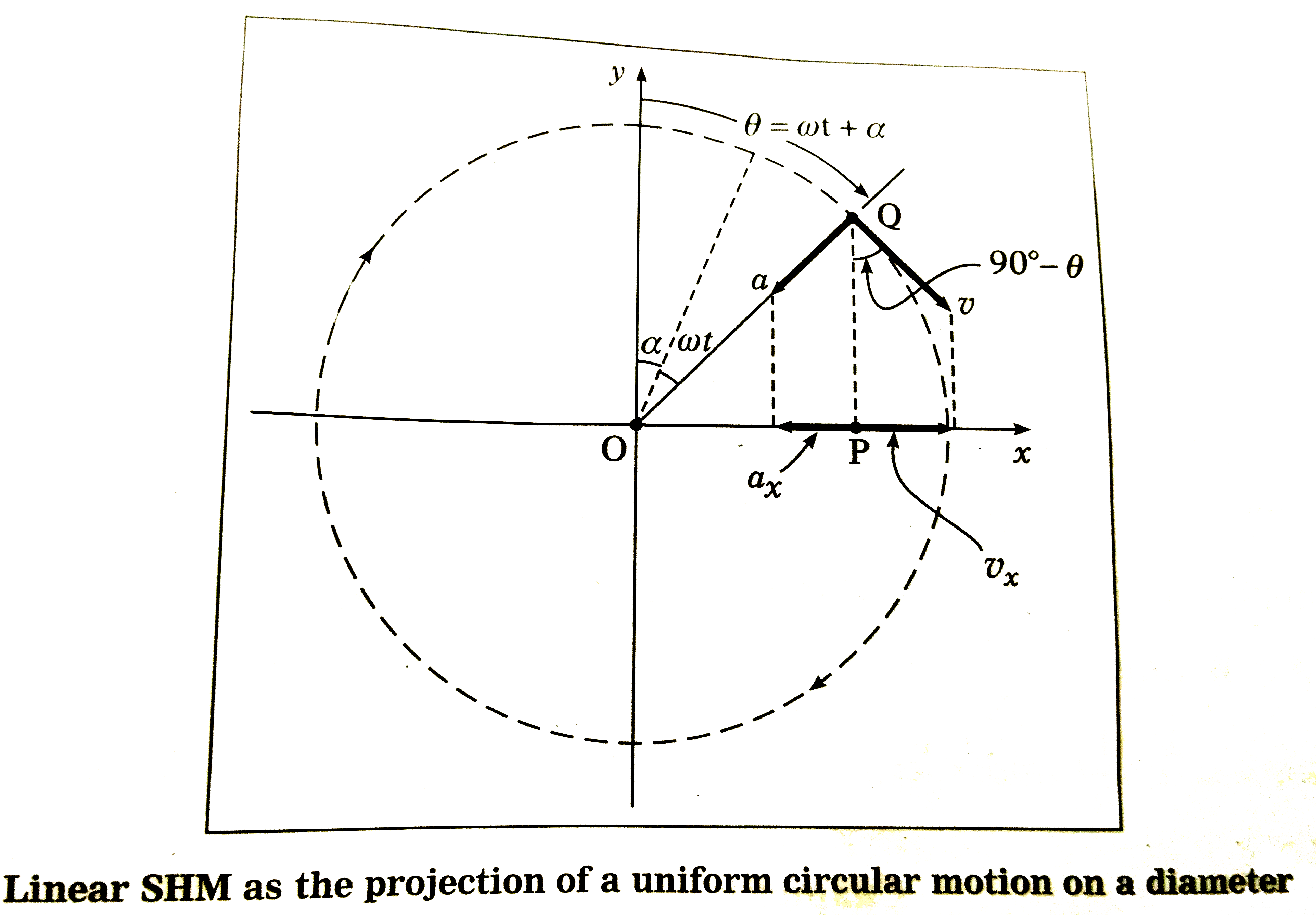
The perpendicular projection of Q onto the x-axis is P. Then as, the particle travels around the circle, P moves to-and-fro along the x-axis. Line OQ makes an angle `prop` with the y-axis at t=0. At time t, this angle becomes `theta=omegat+alpha`.
The projection P of the reference point is described by the x-coordinate,
`x=OP=OQ sin angle OQP." Since "angle OQP=omega t+alpha,`
`x=A" sin "(omega t+alpha)`
The tangential velocity of the refrence particle is `v=omega A.` Its x-component at time t is `v_(x)=omega A" sin "(90^(@)-theta)=omega A cos theta`
`therefore v_(x)=omega A cos (omega t +alpha)`
Tbe centripetal accelertation of the reference particle is `a=-omega^(2)A,` so that its x-component at time t is
`a_(x)= a sin angle OQP`
`therefore a_(x)=-omega^(2)A sin (omega t+alpha)=-omega^(2)x`
These results for x, `v_(x) and a_(x)` correspond to the general expressions for displacement, velocity and acceleration of a particle executing linear SHM. Thus, linear SHM can be described as the projection of uniform circular motion onto a fixed diameter of the circular path.