Obtain a relation between radis of an atom and edge length in the following crystalline solids.
(1)Body - centred cubic crystal.
(2) Face - centred cubic crystal.

Text Solution

Verified by Experts

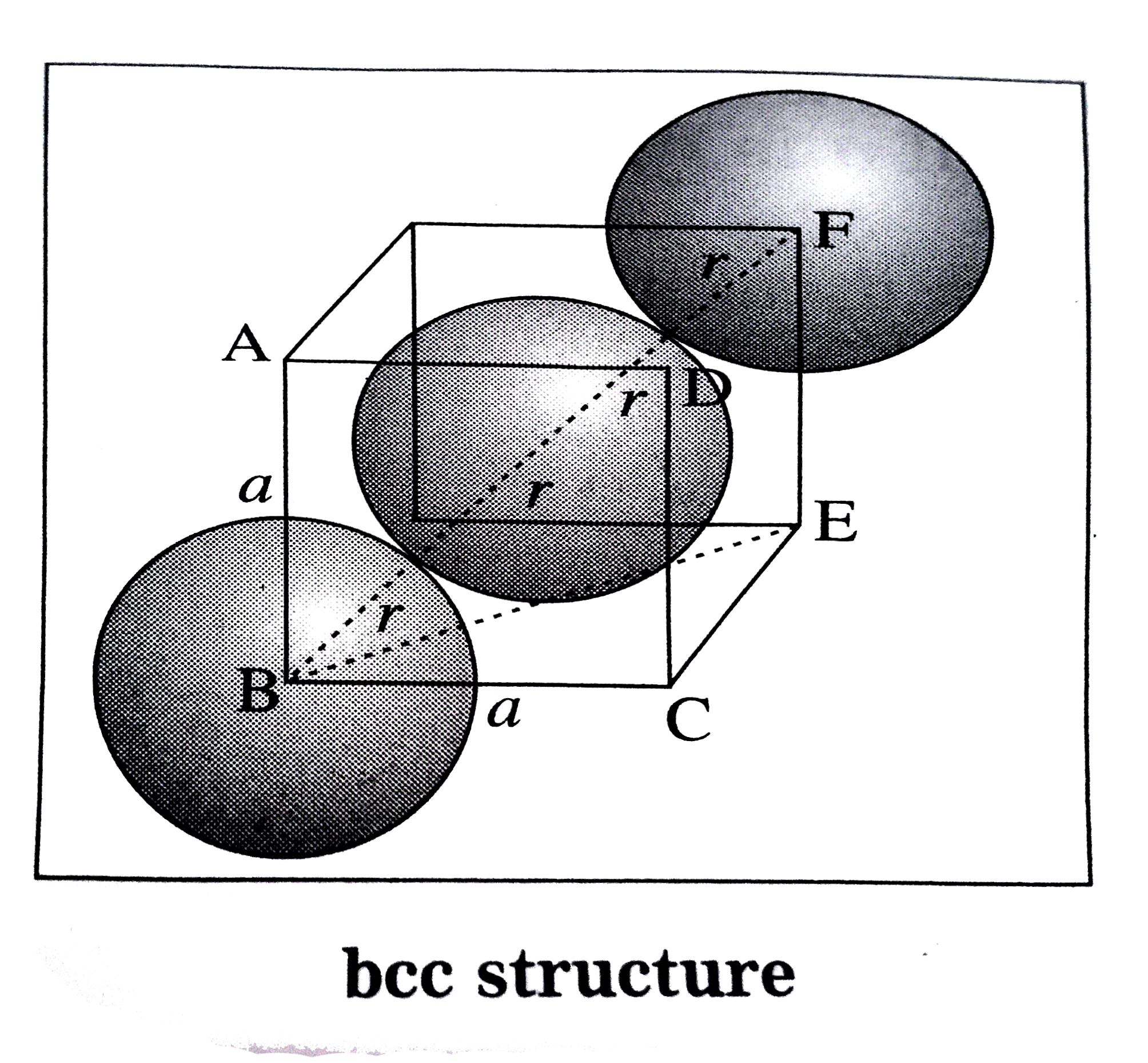
(1) Body-centred cubic (bcc) structure : In this unit cell, 8 atoms are present at 8 corners and one additional atom is present at the body center.
The atmos are in contact along the body diagonal BF. Let a be the edge length and r the radius of an atoms.
Consider a triangle BCE.
$B E^{2} = B C^{2} + C E^{2} = a^{2} + a^{2} = 2 a^{2}$
Consider triangle BEF.
$B F^{2} = B E^{2} + E F^{2} = 2 a^{2} + a^{2} = 3 a^{2}$
$∴ B F = \sqrt{3} a$
From figure , BF = 4r .
$∴ 4 r = \sqrt{3} a$
$∴ r = \frac{\sqrt{3}}{4} a$

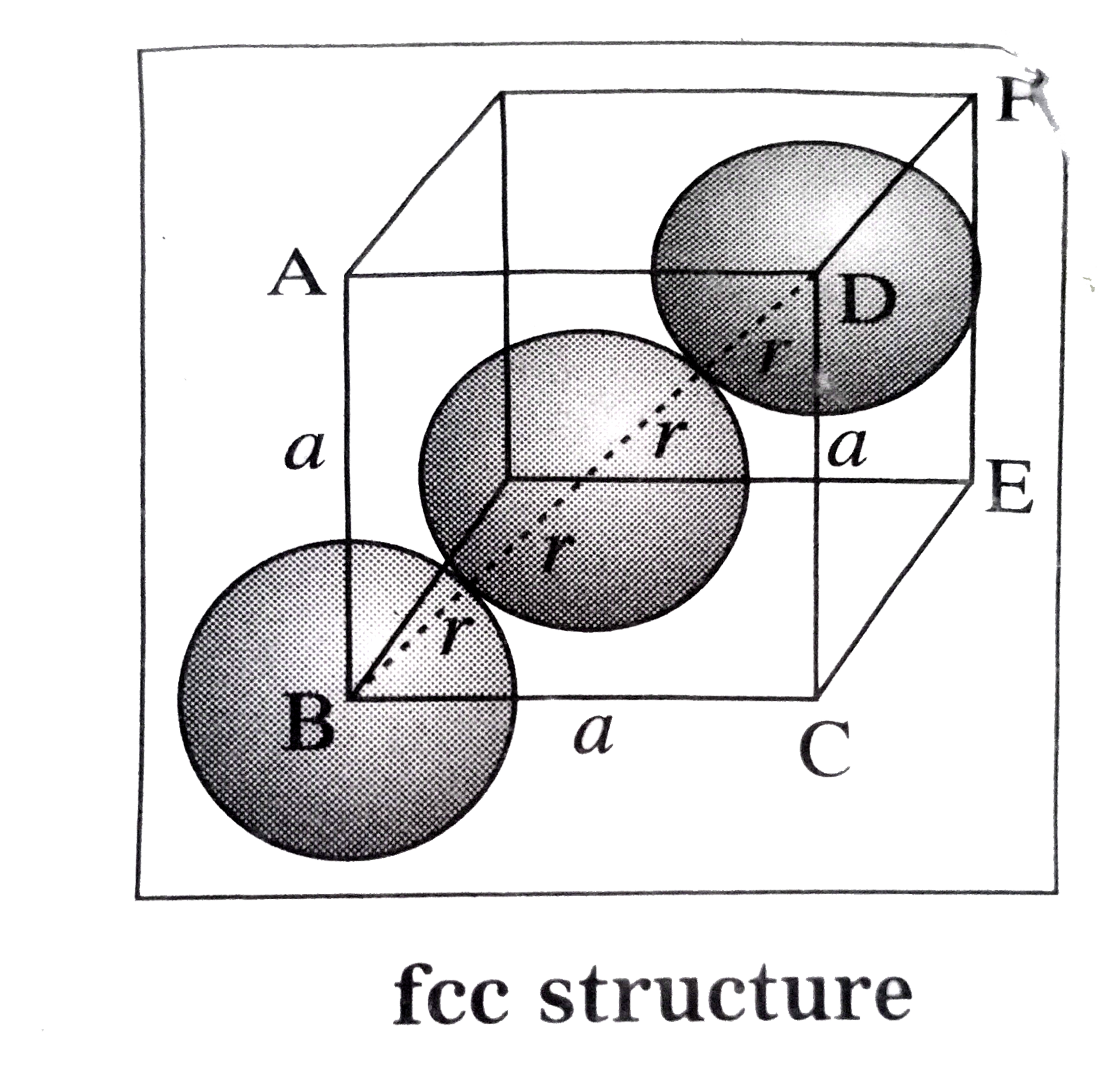
(2) Face-centred cubic (fcc) structure : In the unit cell, there are 8 atoms at 8 coners and 6 atoms at 6 face centre .
The atoms are in contant along the face digaonal BD. Let a be the edge length and r, the radius of an atoms.
Consider a triangle BCD.
$B D^{2} = B C^{2} + C D^{2}$
$= a^{2} + a^{2} = 2 a^{2}$
$∴ B D = \sqrt{2 a}$
From figure BD = 4r
$∴ 4 r = \sqrt{2} a$
$∴ r = \frac{\sqrt{2}}{4} a = \frac{a}{2 \sqrt{2}}$
$r = \frac{a}{2 \sqrt{2}}$

Updated on:21/07/2023

The relation between atomic radius ( r ) and edge length ( a ) a face - centred cubic cell is
A $r = \frac{a}{2}$
B $r = \frac{a}{2 \sqrt{2}}$
C $r = \frac{a \sqrt{3}}{4}$
D $\frac{\sqrt{2} a}{2}$
The relation between atomic radius and edge length 'a' of a body centred cubic unit cell :
A $r = a / 2$
B $r = \sqrt{a / 2}$
C $r = \frac{\sqrt{3}}{4} a$
D $r = \frac{3 a}{2}$
The relation between atomic radius and edge length 'a' of a body centred cubic unit cell :
Ar=a/2
B $r = \sqrt{a / 2}$
C $r = \frac{\sqrt{3}}{4} a$
D $r = \frac{3a}{2}$